Let's solve The Tremendous Tak-Tak Tree.
Let me try to summarise the problem statement: there is a tree which has some number of fruits. This number doubles every full moon. We are asked to write a program that counts the full moons until the number satisfies a certain condition (that is, until the number is a 'good number for a feast').
How would such a program work?
It's always a good idea to try making up a few cases and solving them by hand. You should try picking a few starting numbers and finding the answers for them. For convenience I'll include a couple of examples, but this is really something you should try on your own.
So what's the answer if there are, say, three fruits on the tree at the beginning? It's easy enough to see how the number of fruits on the tree increases with each full moon. It goes: 3, 6, 12, 24, 48, and so on, doubling each time. The tricky part is spotting the first 'good number' in the sequence. Let's try that now.
A 'good number' of fruits can be divided evenly between eleven people with one left over. This isn't possible for 3 and 6 - they're just too small to divide like that. For the number 12, a little fiddling shows this to be 'good'. (We can give each person one fruit, leaving exactly one left over.)
We can try this for a few more cases. Some are easier than others, though: sequences like 25, 50, 100... reach a good number fairly quickly (100 = 9 x 11 + 1), whereas sequences like 24, 48, 96... take a long time to get there, and the numbers get so big that it's not immediately clear whether they divide nicely or not.
Now that we have some idea how to solve these cases by hand, we might try creating a program that does the same thing. To solve the cases ourselves, we did a simulation of sorts: we tracked the amount of fruit after each moon, and stopped when the number was right, just as our fictional villagers would wait month by month for the date of the feast.
We could sum up our algorithm (method) as follows: simulate the tree's growth month by month, until we reach a good number for a feast. Alternately, we might write it in this form:
This leads to two major questions for our implementation: How can we tell if the feast is able to be held? How do we perform the simulation?
Let's deal with these individually.
From the problem statement, the number of fruits on the tree is 'good' if it can be divided evenly into eleven parts with one left over. We need to find a condition - a test that could be encoded into an if statement - that lets us tell good numbers apart from bad ones.
Naturally, since the definition involves division, we'd expect that our solution also involves division in one form or another. This might involve the division operator /, or the modulo operator %. (Recall that a/b gives a divided by b, rounded down, and a%b gives the remainder. Both of these were discussed in the walkthrough for Mixed Fraction.)
To help things along, let's make a list of all the 'good' numbers. We're told that the tree has to contain at least 2 fruits at any given time (since it only ever gains them), so the first good number is 12 = 1 x 11 + 1. The next is 23 = 2 x 11 + 1: it's not hard to show there aren't any in between. Listing a few more, we get:
12 23 34 45 56 67 78 89 100 111 122 133 144 155 166 177 188 199 210 221 232 243...
(Notice that this is an arithmetic sequence: each number is the previous number plus eleven.)
One possibility is to have our program generate a list of good numbers and constantly refer to this list. This works well if the list size is small, but given how big our tree can get, we could conceivably dealing with hundreds of millions of numbers. Our program would have neither the time nor the memory space to work with such a list.
Since we were talking about the / and % operators, we might see what happens when we apply those operators to the numbers in the list.
| x (number) | x / 11 (quotient) | x % 11 (remainder) |
|---|---|---|
| 12 | 1 | 1 |
| 23 | 2 | 1 |
| 34 | 3 | 1 |
| 45 | 4 | 1 |
| 56 | 5 | 1 |
| 67 | 6 | 1 |
| 78 | 7 | 1 |
| 89 | 8 | 1 |
| 100 | 9 | 1 |
| 111 | 10 | 1 |
There are some clear patterns here. Firstly, the value of x / 11 increases by one with each successive number. This makes a little sense, given that our number increases by 11 each time.
Secondly, the value of x % 11 is always 1. This also makes sense - the modulo operator gives us the remainder upon division. Saying "x % 11 is 1" means the same as "x gives a remainder of 1 when divided by 11", which means the same as "x divides evenly into 11 parts with 1 left over". But this is exactly the definition of a 'good number for a feast'!
In summary: the condition (x % 11 == 1) is true when x is a good number and false otherwise.
Our program needs to simulate each full moon until a 'good number' is reached. This will involve repeating an action - the doubling of the fruits - numerous times. To do this, we require something a little different to other problems we have seen so far.
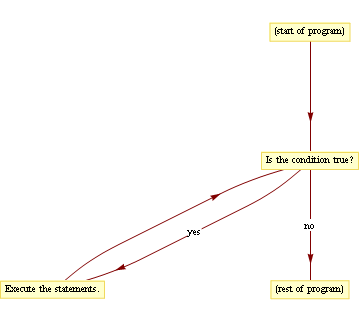
You may have some familiarity with loops: these are programming language features that allow a block of code to be executed more than once. There are many different kinds of loops, depending on your programming language. I want to illustrate one particular kind: the while loop.
In C/C++, they are written something like this:
while (condition) {
statements
}
...where statements refers to any block of normal code, and condition is the same sort of true/false question you would give to an if statement.

When the computer first encounters the while statement, it will check the condition. If the condition is true, it will execute all the statements inside the curly braces, then start again at the while statement. If the condition is false, it will skip over the curly braces and continue functioning as normal.
The code could be sensibly read aloud as 'while the condition is true, do the statements'.
Now, let us return to the problem at hand. The trick to using while loops is to find a way of phrasing our instructions so that they fit nicely into the loop. So far, we have phrased them as 'keep simulating new moons until we reach a good number'.
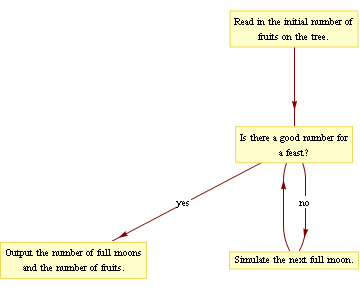
The crude flow chart above illustrates our desired sequence of events. Notice that this resembles, but doesn't quite match, the operation of a generic while loop (the first diagram). Notice that our plain-language description doesn't include the word 'while' - it may need to be rephrased slightly.
Noticing that swapping 'yes' and 'no' yields something better resembling a while loop, we might try negating our condition: asking whether our number is bad instead of good. Then we can phrase our instructions as 'keep simulating new moons while we have a bad number':
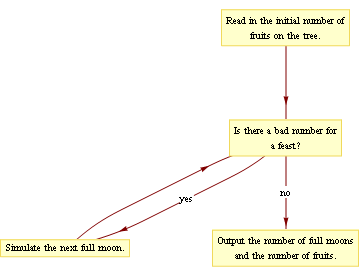
This looks much better. We can immediately begin coding the loop as follows:
while (nFruit % 11 != 1) {
...
}
(Note that this is the direct opposite of the condition we devised in the previous section. This is because we have switched from asking if a number is good to asking if it is bad, or 'not good'.)
Now, the code we want to be repeated goes inside the loop, between the curly braces. In this case, we want to simulate the doubling of the number of fruits on the tree, so we should write one of the following:
nFruit = nFruit + nFruit; nFruit = nFruit * 2; nFruit *= 2;
All of the above lines are equivalent. If you haven't done much programming, they might seem strange, since the equals sign doesn't denote equality like it does in maths. The equals sign is an assignment operator: it instructs the computer to calculate the value on the right hand side, and store it in the variable on the left hand side. Hence "nFruit = nFruit * 2;" makes perfect sense: it tells the computer, "calculate the value of nFruit * 2, and then set nFruit to that value".
Clearly the first and second lines are equivalent. The third line is the special instruction "multiply nFruit by 2". The operators +=, -=, *=, /= and %= are all defined similarly. It's a useful shortcut which saves us writing the variable name a second time, which is especially handy when we're dealing with complicated data structures that make for long variable references.
So far our code looks something like this:
while (nFruit % 11 != 1) {
nFruit *= 2;
}
Our code should correctly calculate the final number of fruits on the tree. Of course, this is only half the problem: we also need to calculate the number of full moons that occur in the process.
We'll need a variable to keep track of this number. I've decided to call it nMoons. How should this variable be updated as the loop progresses?
Initially, we should set nMoons to 0, as in the initial state no full moons have passed. The number of fruits doubles only when a full moon passes, so we should increment nMoons whenever we double nFruit. An updated version of the loop might read:
nMoons = 0;
while (nFruit % 11 != 1) {
nFruit *= 2;
nMoons += 1;
}
Reading this section aloud: "Set the number of moons to zero. Then, while the feast cannot be held, double the number of fruits and increment the number of moons." This sounds like how the simulation ought to work.
This is the essence of the solution. Clearly we'll also need to deal with reading and writing the files, but by this point you should be able to code up a working solution to The Tremendous Tak-Tak Tree.
__END__ $site->putPageFooter(); # Always return true. 1;