
Problem: Snurgle Holders
Want to try solving this problem? You can submit your code online if you log in or register.
Snurgle Holders
Input File: snurgle.in
Output File: snurgle.out
Time Limit: 1 second
Memory Limit: 32 MB
You run a factory that manufactures the highest quality snurgle holders. Such an exquisite product requires exemplary standards of manufacturing, with constant inspection and quality control at each stage of the process.
Snurgle holders are manufactured in multiple steps. Each step requires an alert and highly-trained employee to take some materials, possibly coming from one or more earlier steps, and process them. The output of every step eventually reaches the final step, where the snurgle holders are packaged and taken away to be sold to delighted customers.
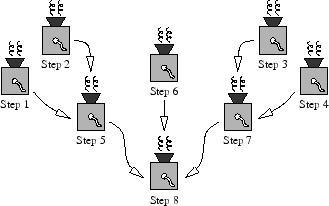
Quality is of paramount importance to you, and so you decide to hire inspectors to watch over your manufacturing process. Ideally you would like to place an inspector at each step of the process, but experience has taught you that more inspectors do not necessarily lead to a higher quality product. In particular, when two inspectors are placed at adjacent steps of the manufacturing process, they start chatting with each other and forget about the snurgle holders entirely. Two steps are considered adjacent if one leads immediately to the other.
For example, in the processing chain illustrated above you can place inspectors at steps 1, 2 and 7 without problems. You cannot place inspectors at steps 1, 3 and 7 since steps 3 and 7 are adjacent. However, you can happily place inspectors at steps 1, 3 and 8 — even though steps 1 and 3 both lead indirectly to 8, there are other steps in between and so the steps are not adjacent.
Your task is to determine the largest number of inspectors that you can hire, assuming that each inspector is placed at a different step and no two inspectors are placed at adjacent steps.
Input
The first line of input will contain a single integer n, representing the number of manufacturing steps required to produce snurgle holders (1 <= n <= 100,000). These steps are numbered 1,2,...,n.
Following this will be (n-1) lines each containing a single integer. The integer on the ith of these lines indicates which step occurs immediately after step i (i.e., where the output from step i is sent to next).
It is guaranteed that each step will only ever lead to a higher step. That is, if step i leads immediately to step j then i < j. Step n is always the final step of the process (and therefore has no corresponding input line).
Output
The output should contain a single integer m, the maximum number of inspectors that can be hired.
Sample Input
8 5 5 7 7 8 8 8
Sample Output
5
Explanation
The sample input corresponds to the diagram above. The largest number of inspectors that can be placed is 5. One such arrangement places inspectors at steps 1, 2, 3, 4, and 8.
Scoring
The score for each input scenario will be 100% if the correct answer is written to the output file, and 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 27 April 2024, 11:47am AEST