
Problem: Wet Chairs
Want to try solving this problem? You can submit your code online if you log in or register.
Wet Chairs
Output File: chairsout.txt
Time Limit: 1 second
Congratulations, contest winner! As a prize for winning the Australian Image Opening Competition you and all your friends are invited to a private concert with the country's finest musical acts.
As luck would have it, it has rained on the morning of the concert. To make matters worse, the staff did a very rushed job drying the seats! Now it is up to you to decide how to seat everyone.
The seats are arranged in a single long line in front of the stage. In particular there are chairs in the line, and each seat is either wet or dry.
However, all is not lost. Out of the N friends you are bringing to the concert K of them are happy to sit on a wet chair. The other N-K of your friends insist on sitting on a dry chair.
Since this concert is best enjoyed with friends, you would also like your group to be seated as close together as possible so that the distance between the leftmost person and rightmost person is as small as possible. Output the smallest distance possible between the leftmost and rightmost friend at the concert.
Your task is to write a program that outputs this smallest possible distance.
Input
The input file will have two lines. The first line of input contains 3 numbers: C N K.
- C is the total number of chairs.
- N is the number of friends to whom you must assign seats.
- K is the number of your friends who are able to sit on either a wet chair or a dry chair.
The second line will have C letters on it, each of which will be either
d or w. These letters represent the line of chairs at
the concert, giving the order of dry and wet chairs. In particular
d is a dry chair, w is a wet chair.
Output
Output should be a single integer, the smallest distance possible between the leftmost and rightmost friend at the concert with no more than K of them sitting on wet chairs.
Sample Input 1
8 4 1 wddwdddw
Sample Output 1
4
Explanation 1
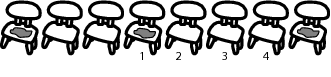
Here we have to seat four friends, one of whom is willing to sit on a wet chair. Fortunately we can seat three of the friends on the group of three dry chairs, and the remaining friend on an adjacent wet chair. The friends can't get closer together than this.
The answer is 4, since there are four chairs from the leftmost to the rightmost friend, including the chair on each end.
Sample Input 2
8 4 0 wddwdddw
Sample Output 2
5
Explanation 2
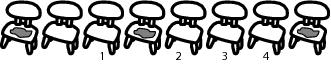
Once again we have to seat four friends, and this time none of them are willing to sit on a wet chair. In this example we can skip over the wet chair in the middle, and sit a friend in the position marked 1 in the diagram. Then we sit the remaining friends in the spots marked 2, 3 and 4.
This is the best arrangement we can have, so the answer is 5.
Sample Input 3
10 6 2 wddwwwdddw
Sample Output 3
7
Explanation 3

Finally, we have to seat six friends two of whom are willing to sit on wet chairs. In this situation there aren't enough friends who can sit on wet chairs to take up the block of three wet chairs. So we can sit two friends on two of the three wet chairs in the middle, three friends on the block of three dry chairs, and the remaining friend on the right chair of the two dry chairs. These are indicated in the diagram by the numbers 1 to 6.
Here the leftmost and rightmost friend are 7 chairs apart.
Subtasks & Constraints
For all subtasks it is guaranteed that:- 1 ≤ N ≤ C ≤ 100,000
- 0 ≤ K ≤ N
- It will always be possible to seat everyone.
Further, for individual subtasks:
- For Subtask 1 (15 marks), C ≤ 100.
- For Subtask 2 (25 marks), C ≤ 3,000.
- For Subtask 3 (30 marks), C ≤ 100,000, K = 0. That is, none of your friends are able to sit on a wet chair.
- For Subtask 4 (30 marks), C ≤ 100,000 and no additional constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 25 April 2024, 8:09pm AEST