
Problem: No Ball
Want to try solving this problem? You can submit your code online if you log in or register.
No Ball
Output File: standard output
Time Limit: 2 seconds
Memory Limit: 512 MB
Today’s the day you retire and you, like all retirees in Graphland, are shipped off to the beautiful country of Flatland. Suddenly flooded with nostalgia, you long for the good ol’ days of playing cricket with your mates, whether it be in high school or at the far too rare reunions that you’ve had since. Of course you also remember the constant struggle to decide who would bring the kit and where you’d all play. You immediately decide to build your new house so that you and your mates will always have a great place to get together and play.
Flatland is a grid with the top row and left most column numbered 0, increasing from top to bottom and left to right. Each of your N friends lives in a cell of the grid. No two friends live in the same cell.
Unfortunately, Flatland is rather large so you will only be able to contact certain subsets of your friends. Specifically, you will be given a choice of Q communication rectangles and will be limited to only contacting the friends in the communication rectangle you choose. A cell (r,c) is inside the communication rectangle with upper-left and lower-right corners (R1,C1) and (R2,C2) respectively when R1 ≤ r ≤ R2 and C1 ≤ c ≤ C2.
You decide to find the best cell to build your house for each communication rectangle. This should be the cell that minimises the sum of the Manhattan distances to all of the friends in that communication rectangle. In case of a tie, pick the cell with the lowest row coordinate, then the lowest column coordinate.
Note that even though no two friends live on the same cell, you are allowed to build your house on top of an occupied cell. (Despite the name, Flatland has at least three dimensions).
Forever being “that friend who is obsessed with coding”, you decide to write a program to find these locations for you.
Input
- The first line of input will contain two space-separated integers N Q, representing the number of friends and the number of communication rectangles respectively.
- The following N lines of input will each contain two space-separated integers ri ci, describing the row and column of your i-th friend’s house.
- The following Q lines of input will each contain four space-separated integers R1 C1 R2 C2, describing the top-left and bottom-right corner of a communication rectangle.
Output
Your program must output Q lines each containing two space-seperated integers: the best row and column to build your house for the corresponding communication rectangle.
Explanation
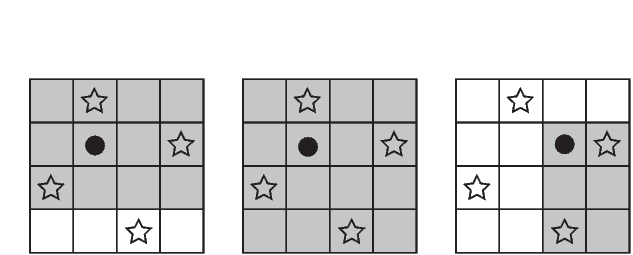
In diagram below, we mark friends’ locations with stars, communication rectangles with grey rectangles, and the ideal location for your house as a black circle.
In the first case, on the left, moving your house to any square results in a greater sum of Manhattan lengths to your friends. In the middle case, the interior 4 squares all have the same sum of Manhattan lengths, however you must output the top most, left most square. In the final case, all squares have the same summed Manhattan distance to your friends, but once again you must choose the top most, left most.
Subtasks & Constraints
For all subtasks, 1 ≤ N ≤ 100000, and 1 ≤ Q ≤ 10000, and 0 ≤ ri, ci, R1, C1, R2, C2 ≤ 1000000000, and R1 ≤ R2 and C1 ≤ C2. Additionally, you are guaranteed there is at least one friend per communication rectangle.
- For Subtask 1 (5 points), 1 ≤ N, Q ≤ 1000, and 0 ≤ ri, ci ≤ 100000.
- For Subtask 2 (10 points), 0 ≤ ci ≤ 100000, and ri = 0 for all of your friends.
- For Subtask 3 (10 points), 0 ≤ ci ≤ 1000000000, and ri = 0 for all of your friends.
- For Subtask 4 (35 points), 0 ≤ ri, ci ≤ 100000 for all of your friends, and R1 = C1 = 0 for all communication rectangles.
- For Subtask 5 (30 points), 0 ≤ ri, ci ≤ 100000.
- For Subtask 6 (10 points), no further constraints apply.
Scoring
The score for each input scenario will be 100% if a correct answer is written to the output file, and 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 26 April 2024, 9:52pm AEST