
Problem: Sculpture II
Want to try solving this problem? You can submit your code online if you log in or register.
Sculpture II
Output File: artout.txt
Time Limit: 1 second
Memory Limit: 1 GB
Following your domination of the fruit sculpture market you've decided to try something new. After hours of thought you've realised the future of art will definitely be BLOCKO, specifically mass produced BLOCKO sculptures.
You've already built the assembly line which consists of a chute at a fixed position dropping BLOCKO blocks onto a conveyor belt below it. The conveyor belt moves right 1 centimetre each second. A sculpture consists of N blocks of BLOCKO, the ith of which will drop ti seconds after assembly begins, have width wi centimetres and height hi centimetres. When a BLOCKO block is dropped it will fall straight down until its bottom edge hits either the conveyor belt or a previously placed BLOCKO block, where it immediately attaches itself to the sculpture. Note that a falling block will not stop moving if it just touches corners with another block. Furthermore when each block is dropped, its right edge will be in line with the right edge of the chute and you may assume it falls into place instantly.
For instance, consider the sculpture consisting of the following 4 blocks. The first block falls after 1 second, is 2 centimetres tall, and 3 centimetres wide.
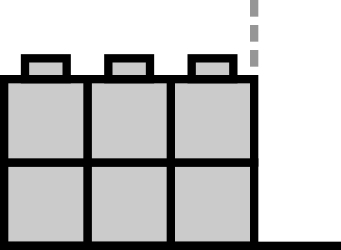
The second block falls after 2 seconds, is 1 centimetre tall, and 2 centimetres wide.

The third block falls after 3 seconds, is 1 centimetre tall, and 2 centimetres wide.

The final block falls after 5 seconds, is 3 centimetres tall, and 1 centimetre wide. Thus the final sculpture will be:

Before you can start shipping your art across the world you must first package it. Specifically you need to determine the maximum height any part of the sculpture will be so that you can order boxes of the correct size. In the above example the sculpture's height is 4 centimetres.
Input
The first line of input will contain a single integer N: the number of blocks in the sculpture.N lines will follow, the ith of which will contain the integers ti, wi, and hi describing the ith block. You may assume that the blocks will be listed in increasing order of time they are placed, that is t1 < t2 < < tN.
Output
Your program must output a single integer: the height of the sculpture in centimetres.
Sample Input
4 1 3 2 2 2 1 3 2 1 5 1 3
Sample Output
4
Explanation
The sample input corresponds to the scenario described above in the problem statement.
Subtasks & Constraints
For all subtasks, 1 ≤ N ≤ 100,000, 1 ≤ ti, wi ≤ 1,000,000, and 1 ≤ hi ≤ 1000 for all i.
- For Subtask 1 (20 marks), ti, wi, N ≤ 1000 and it is guaranteed the the sculpture is at most 1000 centimetres tall.
- For Subtask 2 (20 marks), all blocks have the same wi and the same hi, that is, they all have the same dimensions. Note wi does not have to equal hi, that is, the blocks are not necessarily square.
- For Subtask 3 (60 marks), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 23 April 2024, 7:37pm AEST