
Problem: Carmen Sanfrancisco II: Bank Robbing
Want to try solving this problem? You can submit your code online if you log in or register.
Carmen Sanfrancisco II: Bank Robbing
Output File: whereout.txt
Time Limit: 1 second
Memory Limit: 1 GB
After her foiled attempt to steal the Eiffel Tower, Carmen Sanfrancisco is back, and this time the villainess plans to `rob' several high-profile banks. (The whole banks! You get it? She's gonna steal actual entire buildings!) Fortunately, the ACME Detective Agency is well aware of this plot and has requested your services as an elite detective to track down Carmen's current whereabouts.
You have obtained a map of all the cities in which Carmen Sanfrancisco could currently be hiding. These cities are arranged in a line along a single highway, and it takes an hour to travel from any city to the city directly east or west of it. You know which cities have a bank Carmen is interested in stealing, and you know that once in a city, Carmen takes practically no time to steal a bank (she is a well-prepared master criminal after all).
When Carmen starts moving, the highway patrols will mobilise to close the roads between every city. You know how many hours it will take for the highway patrol to close the road between any pair of adjacent cities, and so does Carmen. Since Carmen won't compromise on the banks she intends to steal, her starting point must be in a city where it's possible for her to reach all the banks before the roads close. Your task is to determine from how many different cities Carmen could begin her heist.
Input
The first line of input will consist of two integers N and C, separated by a space. The first integer N specifies the number of cities. The second integer C specifies the number of cities with a bank that Carmen wishes to steal.Each city is assigned a unique number from 1 to N, numbered from west to east.
The next line of input contains C integers, in ascending order. These are the cities with a bank.
The final line of input contains N - 1 integers, the ith of these ti, representing how many hours it takes to close the road between city i and city i + 1.
Output
Your program must output a single integer: the number of cities from which Carmen Sanfrancisco can begin.
Sample Input
6 3 3 5 6 3 2 2 5 9
Sample Output
3
Explanation
It is possible for Carmen to steal all three banks if she starts from city 2, 3 or 4.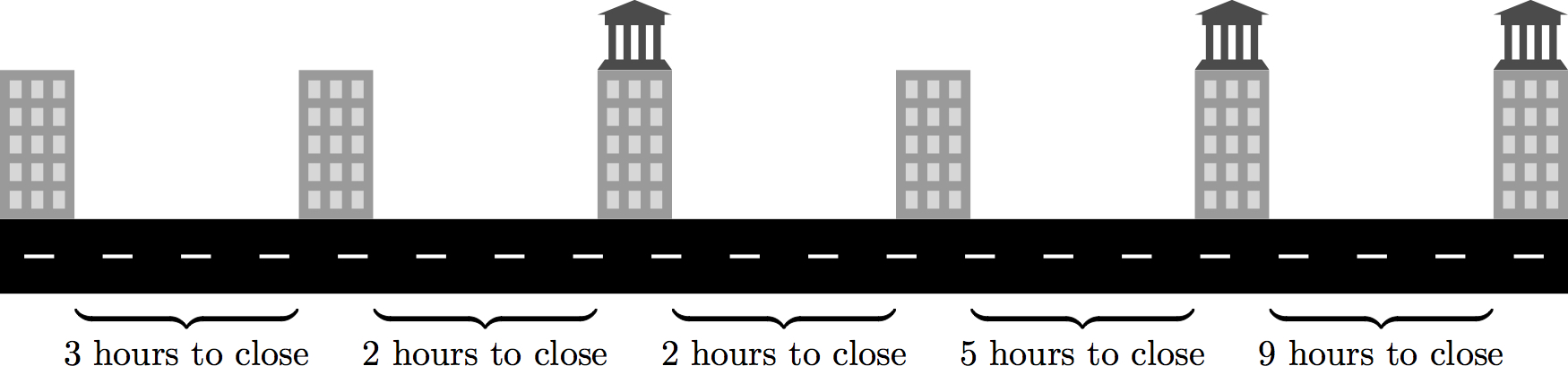
- If Carmen starts in city 1, she can steal the bank in city 3, but the road between city 3 and 4 will close before she can get through to the other two banks.
- If Carmen starts in city 2 or 3, she can keep moving east until she has stolen every bank.
- If Carmen starts in city 4, she can go to the city on the west, then back east again until she has stolen every bank.
- If Carmen starts in city 5, she will not be able to make it to city 3 in time without ignoring city 6.
- If Carmen starts in city 6, she will not be able to make it to city 3 at all.
Subtasks & Constraints
For all subtasks, 1 <= N <= 100,000, 1 <= C <= N, and 0 <= ti < 1,000,000.
- For Subtask 1 (20 marks), 1 <= N <= 1000.
- For Subtask 2 (10 marks), C = 1.
- For Subtask 3 (15 marks), all roads close at the same time.
- For Subtask 4 (55 marks), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 27 April 2024, 9:49am AEST