Problem: Spies

Want to try solving this problem? You can submit your code online if you log in or register.

Spies

Input File: spiesin.txt
Output File: spiesout.txt
Time Limit: 0.1 seconds

It's been a while now since the cold war ended, and you and your friends at the national intelligence agency feel you are missing that spark of danger and excitement in your lives. So you do what any good manager does when things need improving: you rearrange the administrative structure of the Agency.

In the new structure every person has a superior and zero or more subordinates (except for the chair of the Agency who has no superior). Being spies, each person naturally knows nobody other than their superior and their immediate subordinates. This of course means things get hairy when you need to send a message to somebody in a different department – you have no idea how to reach them.

Fortunately for the Agency, the Prime Minister's office has access to all of the secret files and can help you out with your addressing difficulties. Unfortunately they cannot give names, so they merely provide you with instructions such as "send to your superior, then to his superior, then to her second subordinate and finally to her third subordinate." The folks in the Prime Minister's office, however, aren't as sharp as you and your fellow spies, and after that embarrassing incident in which a dinner date was mistakenly offered to the second in command you have been hired to write a program to make sure that the addressing instructions are correct.

Your program must read in the organisational structure of the Agency, a sender and a set of addressing instructions and output the person to whom the message will be delivered.

Each agent has an ID number; if there are N agents then the ID numbers are 1,2,...,N. An address (a set of addressing instructions) is a string of digits such as 0032. The digit 0 means "send to the superior" and the digit k (1 <= k <= 9) means "send to the kth subordinate" (the Agency requires that nobody has more than nine subordinates lest they gain too much power).

Consider the example below, where N = 10. The chair of the Agency is at the top of the tree and each person's subordinates are shown below them. The numbers in the tree are the ID numbers of the agents.

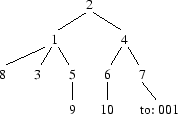
Say a message begins at agent 6 and has address 0013. The message is sent to the superior (4), then to the superior (2), then to the first subordinate (1) and then to the third subordinate (5). Thus the message is delivered to agent 5.

There is one additional complication. Occasionally somebody will move departments, at which point they leave a forwarding address. An example is the first subordinate of 7 in the tree above. Say a message begins at agent 4 and has address 211. The message is sent to the second subordinate (7), then to the first subordinate which is the forwarding address 001. So we follow the forwarding address which takes us up from 7 to the superior (4), the superior (2) and then the first subordinate (1). Now we continue with our original addressing instructions; we were up to the third instruction in 211 which tells us to move from our current position (1) to the first subordinate (8). Finally we have completed our original addressing instructions and we can deliver the message to agent 8.

Input

The first line of the input file will contain the single integer N representing the number of agents (1 <= N <= 300). Following this will be N lines describing agents 1,2,...,N respectively. An agent description will be of the form

sup b s1 s2 ... sb

where sup is the ID number of the superior (or 0 if the agent being described is the Agency chair), b is the number of subordinates that the agent has (0 <= b <= 9) and sX is the ID number or forwarding address for the Xth subordinate. For each sX, an ID number will be written as a plus followed by the subordinate's ID number with no intervening spaces (for instance, +8) and a forwarding address will be written as a minus followed by a sequence of digits with no intervening spaces (for instance, -001).

Following this will be a sequence of queries, each query on its own line. A query will be of the form

ID address

where ID is the ID number of the agent sending the message and address represents the addressing instructions for the message (no preceding dash this time). Following the list of queries will be a line containing the single integer 0. There will be at most 100 queries in the input file.

Each message address and forwarding address will contain at least 1 and at most 15 digits, and there will be no spaces between the digits.

Output

For each query in the input file you must output a single line containing the ID number of the agent who will receive the message. You may assume that all addressing instructions are valid; you will never be asked to pass a message to a subordinate that does not exist or to the superior of the Agency chair, and there will never be an infinite loop of forwarding addresses.

Sample Input

10
2 3 +8 +3 +5
0 2 +1 +4
1 0
2 2 +6 +7
1 1 +9
4 1 +10
4 1 -001
1 0
5 0
6 0
6 0013
4 211
0

Sample Output

5
8

The sample data above describes the tree and the two queries discussed earlier in the problem description.

Scoring

The score for each query in the input file will be 100% if the correct solution is written to the output file and 0% otherwise.