
Problem: Mobiles
Want to try solving this problem? You can submit your code online if you log in or register.
Mobiles
Input File: mobin.txt
Output File: mobout.txt
Time Limit: 1.667 seconds
After several months of quarrelling, your aunt has turned up on your mother's doorstep with a beautiful peace offering. It is a present for your younger brother, who is delighted when he discovers it is an intricate mobile with loud rattling balls and clanking metal rods. He is instantly addicted to the toy, which is a puzzle that requires you to arrange a set of balls of different weights on a set of hooks so that the mobile balances.
After listening to hours of incessant jangling, you decide that your peace of mind is worth more than your brother's educational experience. In an act of frustration you whip out your laptop and begin to write a program that will solve your brother's puzzle for him.
The mobile consists of a series of horizontal rods connected by vertical wires. Some of the rods contain hooks on which you need to hang the balls. The balls are numbered 1,2,..., where the number represents the weight of the ball.
Below is a sample mobile with three balls (thus the balls are
numbered 1,2,3). Each hook is represented by a hash (#).
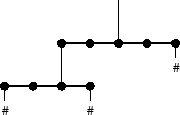
Your task is to make every rod balance. The balance point of each rod is the point at which it is suspended by the wire above it. The torque that a weight applies to a rod is the weight times the distance of the weight from the balance point. A rod balances if the total torque from the weights left of the balance point equals the total torque from the weights right of the balance point.
A sample solution to this example mobile is shown below. Each number represents the weight of the ball that was hung on the corresponding hook.
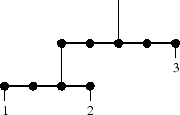
Consider the bottom rod. To the left of the balance point we have ball 1 at distance 2 from the balance point. Thus the torque is 1 x 2 = 2. To the right of the balance point we have ball 2 at distance 1 from the balance point, giving torque 2 x 1 = 2. The torque to the left of the balance point (2) equals the torque to the right of the balance point (2) and so the rod is balanced.
Consider now the higher rod. To the right of the balance point we have ball 3 at distance 2, giving torque 3 x 2 = 6. To the left of the balance point we have a wire holding the lower rod. This lower rod has total weight 3 and the wire that holds it is at distance 2 from the balance point. Thus it has total torque 3 x 2 = 6. We see here that whenever a wire holds an entire branch of the mobile, it is considered as one large weight at the position of the wire that holds it.
Thus for the higher rod the torque to the left equals the torque to the right (both are 6) and so it is also balanced. Because every rod is balanced, we have a solution to the puzzle.
Input
The first line of the input file will be of the form N M where N is the number of balls (2 <= N <= 12) and M is the number of rods (1 <= M <= 9). The mobile will contain N hooks, labelled with the first N letters of the alphabet. The balls will be numbered 1,...,N. The rods will be numbered 1,...,M.
Following this will be M lines describing rods 1,...,M in
order. Each rod description will contain a combination of letters,
numbers, periods (.) and asterisks (*).
These symbols describe the components of the rod from left to right.
A letter indicates a hook on the rod. A number indicates a wire
leading down to another rod (the specific number tells you which rod is
below). An asterisk (each description will have exactly one of
these) represents the balance point. A period (.) indicates
a position on the rod containing nothing of interest. Each rod
description will contain no spaces and will be at most 15 characters
long.
You are guaranteed that rod 1 will be the uppermost rod and that, for all other k, rod k will hang from a rod numbered less than k (for example, rod 4 might hang from rod 2 but will not hang from rod 7). You are also guaranteed that no individual rod will contain more than 6 hooks.
Output
Your output must describe a solution to the puzzle. The output should consist of N lines each containing a single integer. The first line should contain the ball hung on hook A, the second line should contain the ball hung on hook B and so on.
You may assume there is always a solution to the puzzle. If there is more than one solution then any solution will suffice.
Sample Input
3 2 2.*.A B.*C
Sample Output
3 1 2
The sample data above describes the example mobile and its solution as
presented earlier in the problem description. Rod 1 (2.*.A)
represents the upper rod and rod 2 (B.*C) represents the
lower rod.
Scoring
The score for each input file will be 100% if a correct solution is written to the output file and 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 26 April 2024, 10:10pm AEST