Problem: Atlantis

Want to try solving this problem? You can submit your code online if you log in or register.

Atlantis

Input File: atlanin.txt
Output File: atlanout.txt
Time Limit: 0.2 seconds

The Greek philosopher Plato tells us that the ancient continent of Atlantis sank beneath the sea in a single day and night. But you have other ideas. You believe that Atlantis disappeared in a series of small floods, with the waters rising and falling over several years until the continent was completely submerged.

To prove your point, you decide to write a computer program that simulates a single flood as it rises and falls. Your program must read in a rectangular map showing the heights above sea level of the different pieces of land that it contains. An example map is illustrated below.

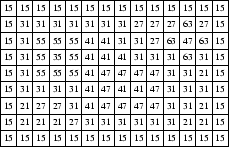
You may assume that the water begins at sea level, and that the sea lies everywhere outside the border of the map. The first stage is the rising of the flood, where the water floods in until it reaches a certain height h. Note that water can only enter from the edges of the map. This is illustrated in the following diagram, with the water rising to height h = 50. The shaded areas show which parts of the map are now underwater. Note in particular that the square near the top left corner at height 35 is not underwater, since it is completely surrounded by high land and the water cannot reach it.

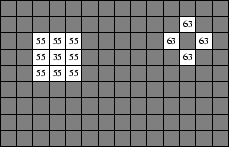
It should be observed that water can flow diagonally as well as horizontally and vertically. For example, near the upper right corner of the illustration above, the water flows in diagonally past the four squares at height 63 to cover the height 47 square situated between them.

The second stage is the falling of the flood, where the water drains away to a final smaller height f. Again the water may only drain away from the edges of the map. The following diagram illustrates the water draining away to final height f = 30, with the shaded areas once more representing land that is underwater. Note that a small lake has formed in the centre of the map — even though the entire lake is at height 41, the water cannot drain away since it is completely surrounded by higher land.

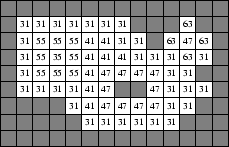
Your overall task is to write a program that will read in a map as well as the two water levels h and f, and output the total number of squares on the map that remain underwater after the water has drained down to its final height f. In this example there are 60 such squares (these are the squares shaded in the final diagram above).

Input

The first line of input will contain the two integers h and f separated by a single space, where h is the initial height to which the water rises and f is the final height to which the water falls. You are guaranteed that h and f will be even numbers satisfying 0 <= f <= h <= 1000.

The second line of input will contain the two integers r and c separated by a single space, where r is the number of rows in the map and c is the number of columns in the map. You are guaranteed that 1 <= r,c <= 100.

Following this will be r lines, each representing a single row of the map. Each of these lines will contain c integers separated by spaces, representing the heights above sea level of the c squares in the corresponding row of the map. Each height will be an odd number between 1 and 999 inclusive.

Output

Your output should consist of a single integer representing the number of squares that remain underwater once the water has fallen to its final height f.

Sample Input

The following input file represents the example discussed above.

50 30
9 14
15 15 15 15 15 15 15 15 15 15 15 15 15 15
15 31 31 31 31 31 31 31 27 27 27 63 27 15
15 31 55 55 55 41 41 31 31 27 63 47 63 15
15 31 55 35 55 41 41 41 31 31 31 63 31 15
15 31 55 55 55 41 47 47 47 47 31 31 21 15
15 31 31 31 31 41 47 41 41 47 31 31 31 15
15 21 27 27 31 41 47 47 47 47 31 31 21 15
15 21 21 21 27 31 31 31 31 31 31 21 21 15
15 15 15 15 15 15 15 15 15 15 15 15 15 15

Sample Output

Scoring

The score for each input file will be 100% if the correct answer is written to the output file and 0% otherwise.