
Problem: Shopping Malls
Want to try solving this problem? You can submit your code online if you log in or register.
Shopping Malls
Input File: mallsin.txt
Output File: mallsout.txt
Time Limit: 0.1 seconds
You have been hired by a company which needs to place an information booth in a shopping mall. The shopping mall also contains four fake trees to add ambience to a shopper's experience. The company wishes to know how many positions the information booth could be placed in, as part of a feasibility study into hiring a consultant to determine the best position for the booth.
Your job is to write a program to determine the number of positions in which the booth can be placed, subject to the following restrictions:
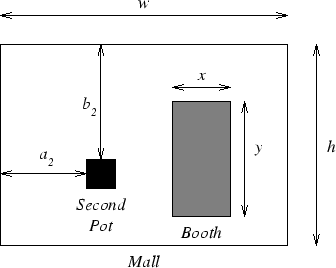
- The mall is rectangular, and measures w metres east-west and h metres north-south.
- The booth is also rectangular, and the architects have determined that it must face the mall entrance and have its walls parallel to the mall. It measures x metres east-west and y metres north-south.
- Due to the cost of custom manufacturing tiles, the booth must be placed an integral number of metres (i.e., 0,1,2,...) from the edge of the mall in both directions, so as to avoid needing to cut any of the metre square tiles used for flooring.
- Militant interior decorators have already decided the locations of the one metre by one metre pots containing the trees. Of course, due to the tiling restrictions, these are also an integral number of metres from the edges of the mall.
- Note that the booth and the pots are allowed to touch any of the walls of the mall.
Input
The input file will contain five lines of integers, separated by spaces, in the following form:
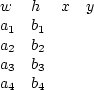
- w is the east-west length of the mall;
- h is the north-south length of the mall;
- x is the east-west length of the booth;
- y is the north-south length of the booth;
- a_1 is the east-west distance in metres from the west side of the first pot to the west edge of the mall;
- b_1 is the north-south distance in metres from the north side of the first pot to the north edge of the mall;
- Similarly for a_2, b_2, a_3, b_3, a_4, b_4, with i representing the locations of the second, third and fourth pots.
You may assume:
- 1 <= w <= 30,000 and 1 <= h <= 30,000 (to account for the possibility of American Megamalls);
- 1 <= x <= w and 1 <= y <= h;
- 0 <= a_i < w and 0 <= b_i < h, for i = 1,2,3,4;
- No two pots will occupy the same position.
All measurements are in metres and are illustrated in the figure below (although this diagram shows only one of the four pots).
Output
The output should consist of a single line containing a single integer, representing the total number of positions in which the booth may be placed.
Sample Input
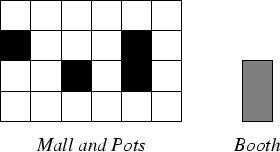
The sample input below corresponds to the configuration shown in the figure above.
6 4 1 2 0 1 2 2 4 1 4 2
Sample Output
11
Scoring
The score for each input scenario will be 100% if the correct answer is written to the output file, and 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 25 April 2024, 6:47am AEST