Problem: Hard Drive

Want to try solving this problem? You can submit your code online if you log in or register.

Hard Drive

Input File: drivein.txt
Output File: driveout.txt
Time Limit: 1.2 seconds
Memory Limit: 10 Mb

You work for a large software company, and your business is operating systems. "No machine too fast," as you say, "we can always give it something more to do!"

With lawsuits alleging that your operating system is unfairly bundled with your virtual toast maker and your electronic encyclopedia of witchcraft, you need to distract the public's attention with a flashy new product. Unfortunately, lawsuits are expensive and so you have had to fire all of your technical staff, leaving you with a company of marketers and managers. After much soul-searching you have hit on a slogan for your new operating system: Divide and Conquer!

In line with your new slogan, your new operating system will partition each hard drive into lots and lots of little pieces. The more partitions, the faster the operating system! You are in charge of designing the advertising brochure, and so you need to know just how many different partitioning possibilities there are.

Your partitioning software works as follows.

It will only work with a hard drive containing 2ⁿ blocks for some n. Initially the hard drive consists of one large partition.
The software may take a partition of size k >= 2 and split it into two equal partitions of size k/2, as illustrated below.
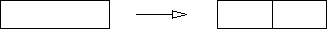
The software may take a partition of size k >= 4 and split it into three consecutive partitions of size k/4, k/2 and k/4 (in that order), as illustrated below.
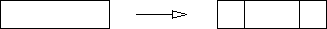
Each partition must consist of an integer number of blocks — you cannot split a block into smaller pieces.

The following diagram illustrates how these operations can be used to split an 8-block hard drive into consecutive partitions of 1, 1, 4 and 2 blocks.

Your task is, given an integer n, to work out how many different ways a hard drive of 2ⁿ blocks can be partitioned. Note that you are only counting the final partitionings — if the same partitioning can be achieved in several different ways using the rules above, you should only count it once.

As an example, the six different ways of partitioning a hard drive of size 2² = 4 are illustrated below.

Since your colleagues who are proofreading the advertising brochure cannot deal with large numbers, your program must output the answer modulo m for some modulus m <= 1000. For example, there are 2350 possible partitionings for a hard drive of size 2⁴ = 16. If m = 100, your program would output the answer 50 in this case.

Hint:
The numbers in this problem can grow extremely large, and so it is recommended that you avoid overflow by reducing modulo m during some of your intermediate calculations. For example, instead of a = b⁵ mod m, you could evaluate a = ((b³ mod m) x (b² mod m)) mod m.

You can evaluate k mod m in C/C++ by writing k % m, and in Pascal you can write k mod m.

Input

Input will consist of a single line containing the integers n and m as described above, separated by a single space. You are guaranteed that 0 <= n <= 10,000,000 and 1 <= m <= 1,000.

Output

Output should consist of a single integer, giving the number of partitionings reduced modulo m as described above.

Sample Input 1

2 100

Sample Output 1

Sample Input 2

4 100

Sample Output 2

Scoring

The score for each input scenario will be 100% if the correct answer is written to the output file, and 0% otherwise.