Problem: Frogs
Want to try solving this problem? You can submit your code online if you log in or register.
Frogs
Input File: frogsin.txt
Output File: frogsout.txt
Time Limit: 2 seconds
Memory Limit: 32 MB
In the land of frogs and waterlilies, the wind blows gently over the water, butterflies flap their wings to cause tropical hurricanes and online frog dating has reached critical mass. Every spring, frogs leap online to meet their future partners. One popular meeting spot is the lake---a dangerous rendezvous location where many frogs have gone missing in the past, said to have been eaten by a local crocodile.
The lake is sprinkled with lily pads. The frogs can leap between lily pads, but due to the recent crocodile sightings, only certain leaps can be made safely. Leaping from one lily pad to another takes precisely one second. Additionally, the frog cannot remain on a lily pad without being potentially eaten by a crocodile, thus as soon as a frog lands upon a lily pad, it must start its move immediately to another one. That is, every second, each frog must travel to a different lily pad.
Alice and Bob are two frogs from different parts of the wetland and plan to meet on the lake one evening. They begin on different lily pads and wish to find each other as quickly as possible, so that they can leap off into the sunset, croaking together.
You have been asked to help Alice and Bob to find their way as quickly as possible to the same lily pad. It does not matter which lily pad this is, but they must arrive on the pad at the same time so that they can leap off into the sunset together. Every second, both frogs must move safely to another lily pad.
Your task is, given the lily pads that can be leaped between safely and the starting lily pads of Alice and Bob, help them be united as quickly as possible.
Input
The first line of the input will contain two integers p j, specifying the number of lily pads, p (2 ≤ p ≤ 100,000), and the total number of possible leaps between lily pads, j (1 ≤ j ≤ 1,000,000).
The second line of the input will contain the starting lily pads of Alice and Bob as two integers Sa Sb. The lily pads are numbered from 1,2,...,p. It is guaranteed that Sa and Sb will not be the same lily pad.
Following this will be j lines, each specifying one possible leap. Each line will contain two integers of the form P1 P2 to indicate that a frog can leap from lily pad P1 to lily pad P2 or vice versa. No possible leap will appear more than once and each lily pad will have at least one leap associated with it.
Output
The output file should contain a single line with two space-separated integers, t m. The integer t specifies the smallest time possible for the two frogs to meet, in seconds. The integer m specifies which lily pad the frogs meet on. There may be multiple pads on which the frogs can meet, in which case you may output any such pad.
If the frogs are unable to meet, then the output should contain a single line containing the string “Broken heart”.
Sample Input 1
9 11 3 7 4 9 2 3 2 1 5 4 3 1 5 6 6 7 9 2 8 6 8 7 7 5
Sample Output 1
3 4
Sample Input 2
5 5 1 4 1 2 2 3 3 4 3 5 5 1
Sample Output 2
Broken heartNote that 3 9 is also a correct output for the first example.
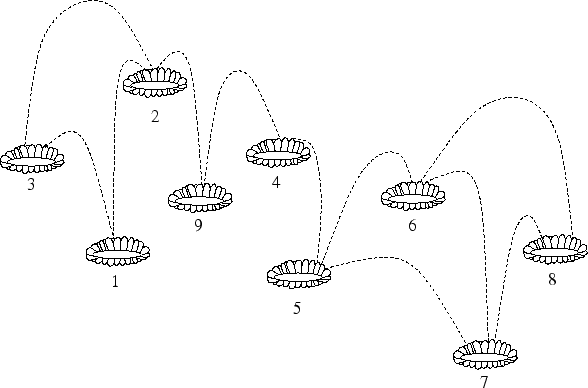
Explanation
The first example corresponds to the diagram below. The two frogs start on pads 3 and 7. The shortest time required to get to the same lily pad is 3 seconds. This can be achieved as follows:- Frog A moves from 3 to 2, Frog B moves from 7 to 6.
- Frog A moves from 2 to 9, Frog B moves from 6 to 5.
- Frog A moves from 9 to 4, Frog B moves from 5 to 4.
- Frog A moves from 3 to 1, Frog B moves from 7 to 5.
- Frog A moves from 1 to 2, Frog B moves from 5 to 4.
- Frog A moves from 2 to 9, Frog B moves from 4 to 9.