
Problem: Clam Oil
Want to try solving this problem? You can submit your code online if you log in or register.
Clam Oil
Output File: clamout.txt
Time Limit: 1 second
Memory Limit: 16 MB
You are the founder of a nation-wide company selling expensive bottles of clam-oil tablets. While your company proudly touts the fantastical qualities of clam-oil (such as longevity, molecular rejuvenation, and protection from ingrown toenails), in practice the tablets tend to achieve little more than afflicting its users with bad breath.
While your business turns a decent profit, it unsurprisingly also receives a large number of complaints from dissatisfied customers. It would be convenient to just ignore such complaints, but too many would cause your business to be investigated by government officials (inevitably causing it to be shut down). Your continued success relies on carefully balancing the number of customers you convince to buy your clam-oil with the number of complaints you receive.
Your business consists of a hierarchy of N salespeople. Each salesperson in the company can have up to two subordinates, and every salesperson (other than salesperson 1—the chief of sales) has a boss.
Your company generates money—and complaints—by sending your salespeople on business trips promoting clam-oil tablets. Careful research has yielded two pieces of information about each salesperson in your company: the amount of profit they earn each time they make a business trip (measured in dollars) and the number of complaints they generate each business trip.
To avoid upsetting the more senior members of your staff, you must ensure that each salesperson goes on at least as many business trips as their immediate subordinates combined. For example, for the corporate structure shown below, if ni is the number of business trips taken by salesperson i, you must ensure that n1 ≥ n2 + n4, n2 ≥ n3, n4 ≥ n5 + n6, and n5 ≥ n7.
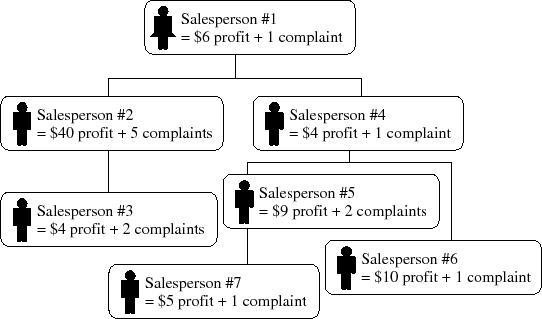
You would like to make as much profit as possible. However, if you receive more than C complaints, your business will be shut down. Your task is to determine the maximum profit you can make without generating more than C complaints.
For instance, consider the previous diagram, assuming that you must not receive more than 9 complaints. One way of using your sales staff is as follows:
- Send salesperson 1 on two business trips, earning 2 × $6 = $12 while generating 2 × 1 = 2 complaints;
- Send salesperson 2 on one business trip, earning $40 while generating 5 complaints;
- Send salesperson 4 on one business trip, earning $4 while generating 1 complaint; and finally
- Send salesperson 6 on one business trip, earning $10 while generating 1 complaint.
In total, this would produce $12 + $40 + $4 + $10 = $66 and generate 9 complaints. This is the most profit you can possibly make.
Input
The first line of input will contain two integers N C separated by a single space (1 ≤ N ≤ 5000, 1 ≤ C ≤ 5000). The first integer N represents the number of salespeople in your company. The second integer C represents the maximum number of complaints you may receive before your business will be shut down.
The second line of input describes the chief of sales (who does not have a boss) and consists of two integers p1 c1. The next N - 1 lines describe the salespeople 2, 3 , ... , N. Each of these lines will be of the form pi ci ai. The value pi is the amount of profit the salesperson will generate each time they take a business trip, while the value ci is the number of complaints they will generate each business trip. The value ai specifies the salesperson's boss.
You are guaranteed that 1 ≤ pi ≤ 100,000, 1 ≤ ci ≤ 5000, and 1 ≤ ai < i.
Output
The output file should consist of a single integer, the maximum amount of profit (measured in dollars) it is possible to make without receiving more than C complaints.
Sample Input 1
7 9 6 1 40 5 1 4 2 2 4 1 1 9 2 4 10 1 4 5 1 5
Sample Output 1
66
Sample Input 2
2 15 5 4 3 2 1
Sample Output 2
18
Subtasks
- For Subtask 1 (40 points), N ≤ 50.
- For Subtask 2 (60 points), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 20 April 2024, 12:32am AEST