
Problem: The Terrifying Canary-Bird
Want to try solving this problem? You can submit your code online if you log in or register.
The Terrifying Canary-Bird
Output File: birdout.txt
Time Limit: 2 seconds
Memory Limit: 32 MB
Fear and pandemonium have struck the hippopotami of North Yorkshire! A monstrous creature from the wilderness of Australia has found its way to the county. It is a horrifying yellow-green winged beast, over half a foot tall. The hippos have dubbed it The Terrifying Canary-Bird. They cower whenever its wings darken the skies, and worse still, the fear is making them lose their appetites.

The hippopotami sleep in the Great Glen, which may be thought of as an R by C grid of squares of varying heights. The Great Glen is rather hilly - no two adjacent squares (squares sharing an edge) have the same height. The Terrifying Canary-Bird regularly swoops across the grass of the Great Glen, terrorising all the hippos it passes.
As part of their grand plan to scare the Terrifying Canary-Bird away from North Yorkshire forever, the hippos set out to study the Canary-Bird's movements closely. Based on many weeks of careful note-taking, the hippos have constructed a formal mathematical definition for a canary-bird path.
A canary-bird path is a sequence of 1 or more squares such that:
- The first square is a local maximum: it has no adjacent square higher than it. (The Terrifying Canary-Bird knows no fear of heights.)
- Each square is adjacent to the square before it. (The Terrifying Canary-Bird cannot teleport... thankfully.)
- Each square has a lower height than the square before it. (The Terrifying Canary-Bird has a small problem in that it cannot fly, only glide and slowly drift downwards.)
- The last square is a local minimum: it has no adjacent square lower than it. (The Terrifying Canary-Bird keeps flying until it can fly no more.)
Your task is to write a program that takes as input a description of the Great Glen and outputs the number of possible canary-bird paths, modulo 1,000,003.
Input
- The first line of input will contain the integers R and C, separated by a space (1 ≤ R,C ≤ 1,000).
- The following R lines will contain C integers each, representing the heights of the various squares of the Great Glen. Each of these integers will be between 1 and 1000000, inclusive.
Output
Output should consist of a single integer, the number of possible canary-bird paths modulo 1,000,003.
Sample Input
2 3 7 6 7 6 8 9
Sample Output
5
Explanation
The local maxima are the top-left and bottom-right squares. The local minima are the squares of height six. The five canary-bird paths are shown below.
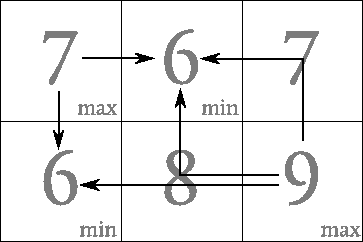
Scoring
The score for each input scenario will be 100% if the correct answer is written to the output file, and 0% otherwise.
For 30% of the available marks, R, C ≤ 50.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 24 April 2024, 10:25am AEST