
Problem: Snap Dragons II
Want to try solving this problem? You can submit your code online if you log in or register.
Snap Dragons II
Output File: snapout.txt
Time Limit: 1 second
Have you ever heard of Melodramia, my friend? It is a land of magic forests and mysterious swamps, of sprinting heroines and dashing heroes. And it is home to two dragons, Rose and Scarlet, who, despite their competitive streak, are the best of friends.
Rose and Scarlet love playing snap tag, a game for two players on an grid. The game goes as follows:
- The two dragons start on different squares.
- It's Rose's turn first. On her turn she must move to an adjacent square (i.e. she must make one step left, right, up, or down).
- It's Scarlet's turn next. On her turn she must move to an adjacent square.
- The two dragons continue alternating turns...
- ...until one dragon lands on the same square as another. When this happens, the dragon who moved last shouts `Snap tag!' and wins the game.
Rose and Scarlet are both snap tag experts and always find a winning strategy if one exists. If it is not possible for either player to gain the upper hand, then the game goes on forever.
In this task, you are given the size of the grid and the starting locations of both dragons. You must write a program to determine how the game ends: Does Rose win? Does Scarlet win? Does the game go on forever?
Input
The input file will contain six space separated integers on a single line, in the format: R C rROSE cROSE rSCARLET cSCARLET where:
- R and C are the number of rows and columns in the grid, respectively;
- rROSE and cROSE are the row and column of Rose's starting square (rows are numbered 1 to R from top to bottom; columns are numbered 1 to C from left to right); and
- rSCARLET and cSCARLET are the row and column of Rose's starting square.
Output
Output should consist of a single upper-case word with no punctuation.
- If Rose can guarantee herself a win, output
ROSE. - If Scarlet can guarantee herself a win, output
SCARLET. - If neither player can guarantee a win, output
DRAW.
Sample Input 1
2 3 1 1 2 3
Sample Output 1
ROSE
Explanation
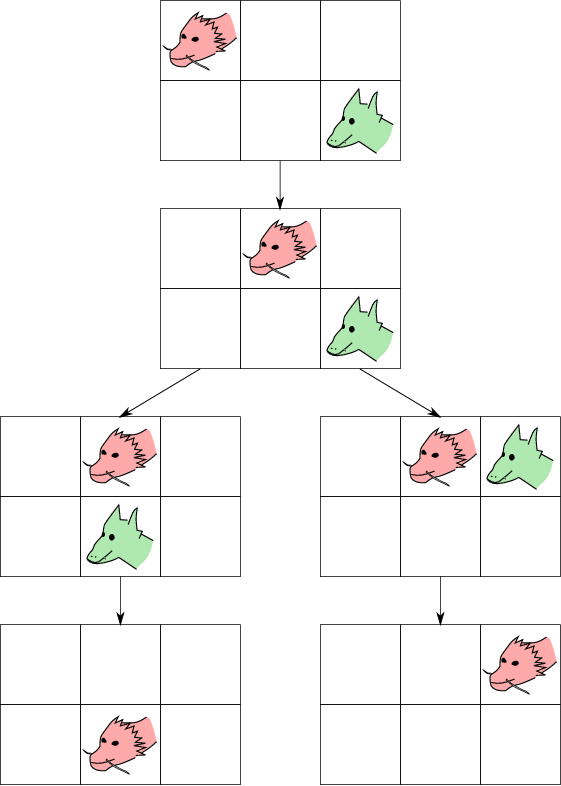
In the first example, Rose can guarantee herself a win if she is clever and cautious.
On her first move, Rose steps to the right. Then, no matter whether Scarlet goes up or left on her turn, Rose can tag her the next turn.
Sample Input 2
5 1 2 1 4 1
Sample Output 2
SCARLET

Explanation
In the second example, Scarlet can guarantee herself a win if she is clever and cautious.
If Rose moves down, then Scarlet will tag her on her very next turn. Otherwise, if Rose moves up, then Scarlet moves up and Rose will be forced to move down next to Scarlet, who will tag her the next turn.
Sample Input 3
15 15 3 5 12 13
Sample Output 3
ROSE
Explanation
In the third example, Rose can guarantee herself a win if she is clever and cautious.
Subtasks & Constraints
- For Subtask 1 (25 marks), R = 2 and C = 2. In other words, if your program always produces the correct solution for a 2 by 2 grid, you will receive at least 25 marks for this problem.
- For Subtask 2 (25 marks), 1 ≤ R ≤ 100 and C = 1.
- For Subtask 3 (40 marks), 1 ≤ R, C ≤ 100.
- For Subtask 4 (10 marks), 1 ≤ R, C ≤ 1,000,000,000.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 20 April 2024, 12:37pm AEST