
Problem: Ruckus League
Want to try solving this problem? You can submit your code online if you log in or register.
Ruckus League
Output File: ruckusout.txt
Time Limit: 1 second
It's that time of year again! The Annual Ruckus World Championships is fast approaching and you are absolutely determined to see Australia victorious. As the name implies, the goal of the competition is to be as loud and obnoxious as possible. Players compete in teams of at least M people (there is no upper limit on team sizes). To make sure teams don't mix, team members must hold hands with each other.
Of course, you've found that there is nothing more obnoxious than spoilt kindergarteners, so you've rounded up N of the loudest ones you could find. You were hoping to send as many teams as possible, but some of the children have already started holding hands with their friends. Being as stubborn as they are, you are finding it rather difficult to convince them to let go of each other, or even to hold hands with anyone else.
Now for any other person, the story would end here; you'd have to send whatever teams their 'friendships' have forged. However, being the social engineering master you are, you've brought K lollipops to use to bribe the children. You can pass a lollipop to the hand of a child, which will make them let go of the hand they are holding.
Using your K lollipops, what is the largest number of teams with at least M children you can form?
Input
The first line of the input file will contain four space separated integers on a single line, in the format: N L K M.
- N is the number of children you have gathered.
- L is the number of pairs of hands that are already joined together.
- K is the number of lollipops you have.
- M is the minimum size of a team. All teams must have at least M people.
The following L lines will each contain two integers, in the format: li ri. This indicates that the lith child's left hand is holding the rith child's right hand. The children are numbered from 1 to N. No one can hold their own hands.
Output
Output should consist of a single integer: the maximum number of teams with at least M children you can form.
Sample Input 1
8 6 0 1 1 2 4 6 5 4 2 3 7 5 6 7
Sample Input 1
3
Explanation
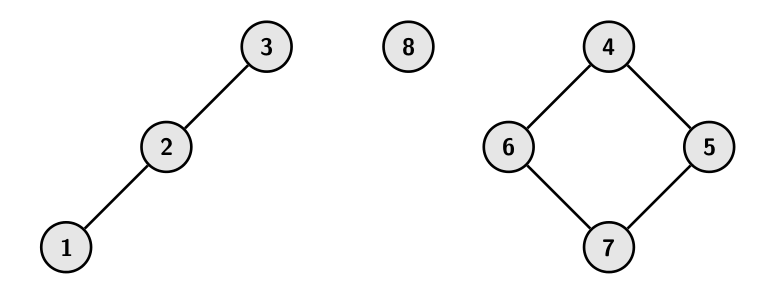
In the first example, you cannot break up any pair of hands (since you
have no lollipops), and teams can have any number of people in them. Initially,
the children have formed three teams: one of size 3, one of size 4 and
one of size 1. Thus the output should be 3.
Sample Input 2
15 13 5 2 1 2 2 6 6 10 10 7 8 9 9 8 3 4 4 5 15 11 11 12 12 13 13 14 14 15
Sample Input 2
6
Explanation
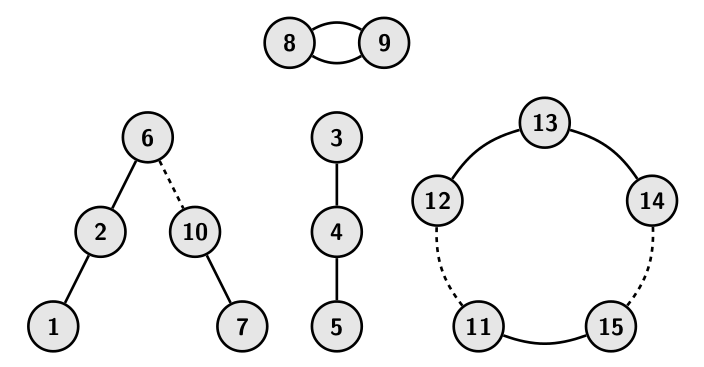
In the second example, each team needs at least 2 people. Currently there
are four teams of size 2, 3, 5 and 5. (The team of size 2 consists of
children 8 and holding both hands with each other.)
By breaking the friendships 6-10, 14-15 and 11-12, we can create up to
six teams, of size 2, 2, 2, 3, 3 and 3. Thus the best answer is 6.
Note that even though we have 5 lollipops, we don't have to use them all in order to make the maximum number of teams (even though we can).
Subtasks & Constraints
For all subtasks, 0 ≤ L ≤ N, 1 ≤ M ≤ N and 0 ≤ K ≤ L.- For Subtask 1 (20 marks), K = 0, M = 1 and N ≤ 1,000.
- For Subtask 2 (20 marks), K = 0 and N ≤ 100,000.
- For Subtask 3 (20 marks), N ≤ 100,000 and everybody is holding hands with exactly two other people.
- For Subtask 4 (20 marks), N ≤ 100,000. Additionally, if the ith person is holding hands with two people, then they are holding hands with one person with a number less than them and one with a number greater. If they are holding hands with one or no person, this condition does not apply.
- For Subtask 5 (20 marks), N ≤ 100,000 and no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 25 April 2024, 7:14pm AEST