
Problem: Balancing Aeroplanes II
Want to try solving this problem? You can submit your code online if you log in or register.
Balancing Aeroplanes II
Output File: balanceout.txt
Time Limit: 1 second
Memory Limit: 1 GB
The recent release of AIOC (Autonomous Infinitesimal Omnipresent Creature) GO has taken the world by storm, and the postal networks everywhere are overloaded trying to deliver all the plush toys that excited players have ordered, from the common Owtwem to the legendary Tabuz. Unfortunately, the shipping company you work for has run out of modern cargo planes, and many more boxes remain unshipped to their impatient recipients!
The only plane left in the hangar is very old, and will only fly safely if the weight of the boxes stacked inside is distributed symmetrically -- the boxes must be placed in the plane in a line of stacks such that the leftmost stack is equal in weight to the rightmost stack, the second leftmost is equal to the second rightmost, and so on.
As chief Alignment Imposition Officer, the task falls to you to ensure the safety of the flight. The boxes in the warehouse are already arranged into a line of stacks, and all boxes are the same size and weight. Since you never quite figured out how to use that forklift properly, you decide to save time by repeating the only operation you know: picking up one whole stack of boxes, and placing it on top of an adjacent stack. You do this until the line of stacks is symmetrical.
In order to escape the wrath of impatient customers, you decide to speed up this process. You whip out your trusty laptop and begin to write a program to calculate the minimum number of forklift operations that must be performed to achieve a symmetrical arrangement.
Input
The first line of input will contain a single integer S: the number of stacks in the warehouse.The second line will contain S space-separated integers, the ith integer ni representing the number of boxes in the ith stack.
Output
Your program must output a single integer: the minimum number of times you will need to pick up a stack of boxes and place it on top of another stack in order to achieve a symmetrical arrangement. Note that it is always possible to achieve such an arrangement by placing all the boxes into a single stack.
Sample Input
10 1 1 1 2 4 2 2 1 2 2
Sample Output
4
Explanation

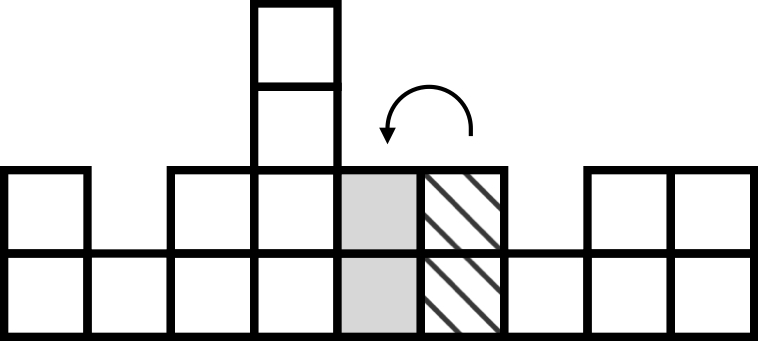
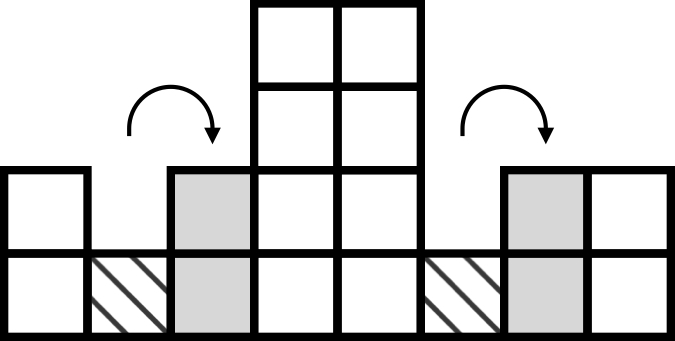
Finally, you place the second stack onto the third, and the sixth onto the seventh, completing the symmetrical arrangement.

This takes four forklift operations in total, which is the least number required to achieve symmetry.
Subtasks & Constraints
For all subtasks, 1 <= S <= 100,000, and 0 < ni <= 10,000 for all i.
- For Subtask 1 (10 marks), it will only be necessary to place a stack of boxes on top of another at most once.
- For Subtask 2 (20 marks), S <= 10.
- For Subtask 3 (20 marks), all ni will be either 1 or 2.
- For Subtask 4 (20 marks), ni <= 500.
- For Subtask 5 (30 marks), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 27 April 2024, 12:43pm AEST