
Problem: Lollipops, Sweets and Chocolates
Want to try solving this problem? You can submit your code online if you log in or register.
Lollipops, Sweets and Chocolates
Output File: lscout.txt
Time Limit: 1 second
Memory Limit: 1 GB
The little boys and little girls of Sydney are excited about the opening of LOLLIPOPS, SWEETS AND CHOCOLATES (LSC), a world renowned candy shop! There are going to be N new branches of LSC opening along the Australian Ice-cream and Oreo Crescent (AIOC). There are L positions on the crescent, each of which can be represented by a number between 1 and L. To promote this, the organisers prepared personalised pamphlets so that for each position on the crescent, the pamphlet lists the N branches in order of how close each shop is to that position. If there are ties, the shops could be listed in any order.
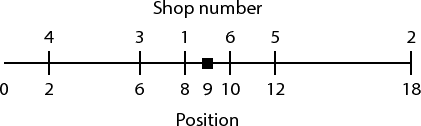
For example, in the diagram above the pamphlet at position 9 could read:
Shop 6: distance 1km
Shop 1: distance 1km
Shop 3: distance 3km
Shop 5: distance 3km
Shop 4: distance 7km
Shop 2: distance 9km
As you were daydreaming about the mouthwatering chlorosulfonic acid sorbet you had last time, you accidentally stepped on a LSC pamphlet! Unfortunately, the stain from your shoe covered up all the distances to the LSCs. In order to satisfy your curiosity, you wish to find a possible position where this pamphlet could have originally been handed out. However LSC is not renowned for their pamphlets' accuracy, so it could be the case that there are no possible positions from where the flyer could have originated.
Input
The first line of input will contain two integers N and L: the number of new LSCs and the number of positions on the crescent respectively.The next line of input will contain N integers, the ith of which describes the position of the ith shop. For each shop, you are guaranteed that the position of that shop will be an even integer.
The next line of input will contain a permutation of the integers 1 to N: a list of these shops sorted in increasing order based on the distance from the position at which the pamphlet was handed out.
Output
Your program must output a single integer: a possible position where the pamphlet could have been handed out, or -1 if you think this pamphlet is incorrect. If there are multiple correct answers, output any of them. Note that a position is only possible if it lies on the crescent with a position between 1 and L inclusive.
Sample Input 1
6 18 8 18 6 2 12 10 6 1 3 5 4 2
Sample Output 1
9
Sample Input 2
4 10 2 4 6 8 2 4 1 3
Sample Output 2
-1
Explanation
Sample input 1 corresponds to the scenario described above in the problem statement. From position 9, shop 1 and 6 are 1 unit away, shop 3 and 5 are 3 units away, shop 4 is 7 units away and shop 2 is 9 units away. In sample input 2, there is no position that is consistent with the positions of the shops.
Subtasks & Constraints
For all subtasks, 1 ≤ L ≤ 109 and 1 ≤ N ≤ 100 000. Further, all the positions of shops will be distinct.
- For Subtask 1 (35 marks), L ≤ 1000, N ≤ 100.
- For Subtask 2 (15 marks), N ≤ 100.
- For Subtask 3 (10 marks), all gaps between adjacent stores will be identical.
- For Subtask 4 (10 marks), all gaps between adjacent stores will be at most 4.
- For Subtask 5 (30 marks), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 19 April 2024, 8:19am AEST