
Problem: Cloud Cover
Want to try solving this problem? You can submit your code online if you log in or register.
Cloud Coverage
Output File: cloudout.txt
Time Limit: 1 second
Memory Limit: 1 GB
During lunch you and your friends were playing your favourite game `stand along a line' when a huge cloud blew overhead. So you got to wondering, how long could that cloud have been? You immediately noted down how far apart each of your friends were standing from one another along the line, and the maximum number that were simultaneously underneath the cloud.
Note that if two people are exactly separated by the length of the cloud, then only one of them can be covered by the cloud at a time. Thus if a cloud is 5 metres long, and two people are standing 5 metres apart, the cloud is only able to cover one of them at a time.
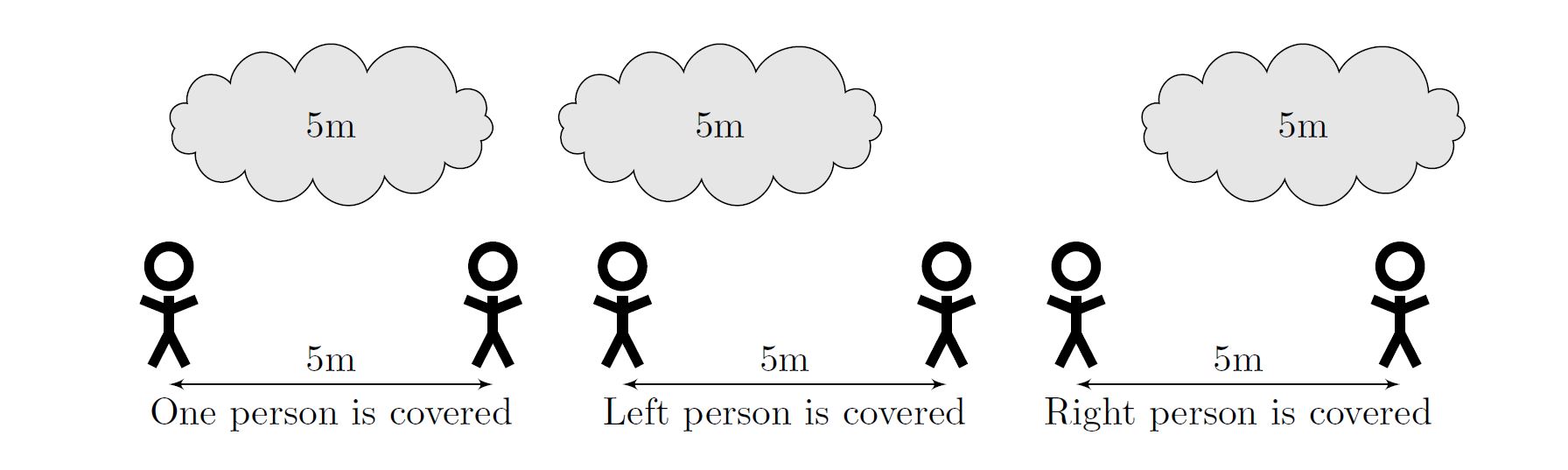
You must now determine the maximum length the cloud could have been, taking into account the maximum number of people it covered simultaneously.
Input
The first line will contain the number of people standing along the line, N, followed by the maximum number covered at any time by the cloud K.The following N-1 lines contain the successive distances between the N people playing the game. These will always be integers.
Output
The maximum length the cloud could have been given that it never covered more than K of your N friends.
Sample Input
6 3 3 6 4 2 5
Sample Output
11
Explanation
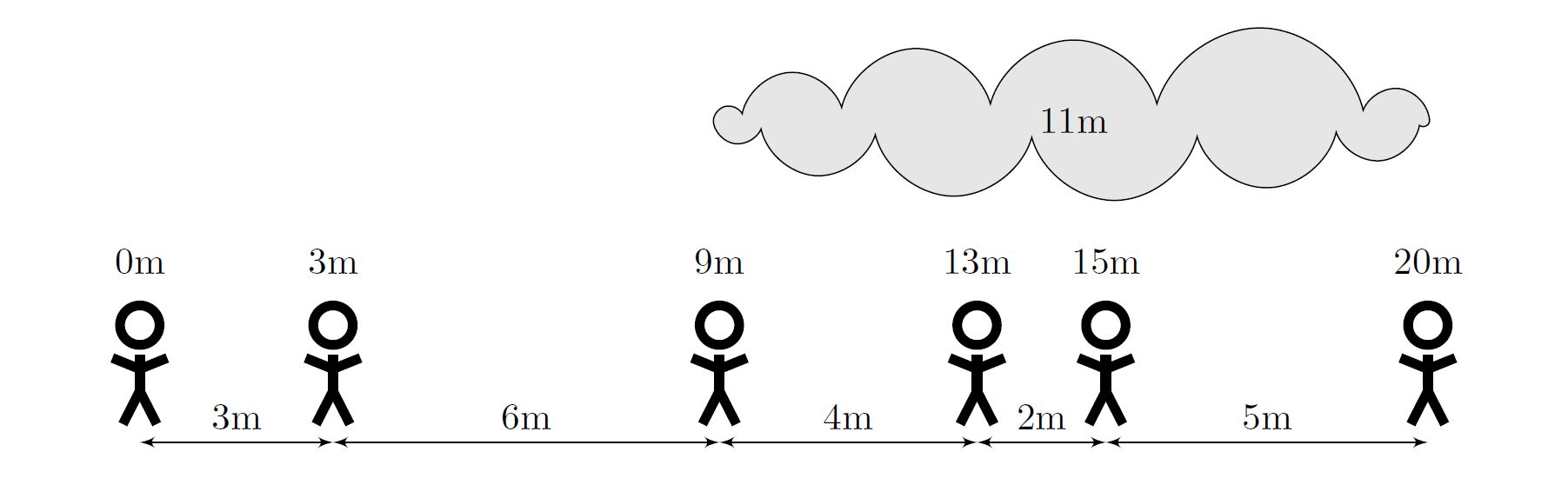
Subtasks & Constraints
For all cases 1 ≤ K < N ≤ 100,000. Note that this means that 2 ≤ N. Further, let us call the distance between the first and last person in the line D. D ≤ 1,000,000,000. Finally, all distances between people will be at least 1.
- For Subtask 1 (20 marks), D ≤ 500, N ≤ 100.
- For Subtask 2 (10 marks), K = 1.
- For Subtask 3 (10 marks), K = 2.
- For Subtask 4 (20 marks), D ≤ 5,000, N ≤ 100.
- For Subtask 5 (15 marks), N ≤ 5,000.
- For Subtask 6 (25 marks), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 20 April 2024, 3:10pm AEST