
Problem: Janitor
Want to try solving this problem? You can submit your code online if you log in or register.
Janitor
Output File: janitorout.txt
Time Limit: 1 second
Memory Limit: 1 GB
Congratulations! You have been appointed head bathroom janitor of your school! Okay, okay, I know you're not thrilled, but somebody has to do it. We thank you for your sacrifice.
The bathroom floor is covered in a rectangular grid of tiles. No one is watching you very closely, so pouring a bucket of water over the floor is enough to make it look like you cleaned it. There is one small problem. The floor is uneven, so depending on which tile you pour the water on, some tiles may not become wet at all, and your deception will be exposed.
Water can flow from any square to any adjacent square of lower height, where adjacent squares may be to the north, south, east or west (water cannot flow across diagonals).
To finish your chore as soon as possible, you've decided to find out what is the fewest number of tiles you need to pour water on to make sure every tile becomes wet.
To complicate matters further, the bathroom is undergoing some hasty renovations. Each day, a tradie will replace one of the tiles, changing its height. After each replacement, you will need to figure out again how many tiles you need to pour water on.
Input
- The first line of input contains three space-separated integers, R,
C, and Q. There are R rows and C columns of tiles and there
will be Q replacements made by the tradies.
- The next R lines each contain C space-separated integers, giving
the initial heights of the tiles. The tradie did such a terrible job
at tiling the bathroom that literally no two adjacent tiles have the
same height, even after any replacements.
- The following Q lines each contain three integers ri, ci and hi. This indicates that the tradies have replaced the tile situated in row ri and column ci with a tile of height hi. Rows are labelled from 1 to R (from top to bottom) and columns are labelled from 1 to C (from left to right).
Output
The output should contain Q+1 lines. The first line should contain the fewest tiles you need to pour water on to make sure every tile gets wet before any replacements are made. The next Q lines should correspond to the Q tile replacements. After each replacement has been made (including all previous modifications), your program should write one line containing the fewest tiles you need to pour water on to make sure every tile gets wet.
Sample Input
3 4 3 5 3 2 0 4 8 4 3 5 7 6 1 2 3 1 3 1 2 2 3 9
Sample Output
2 3 3 2
Explanation
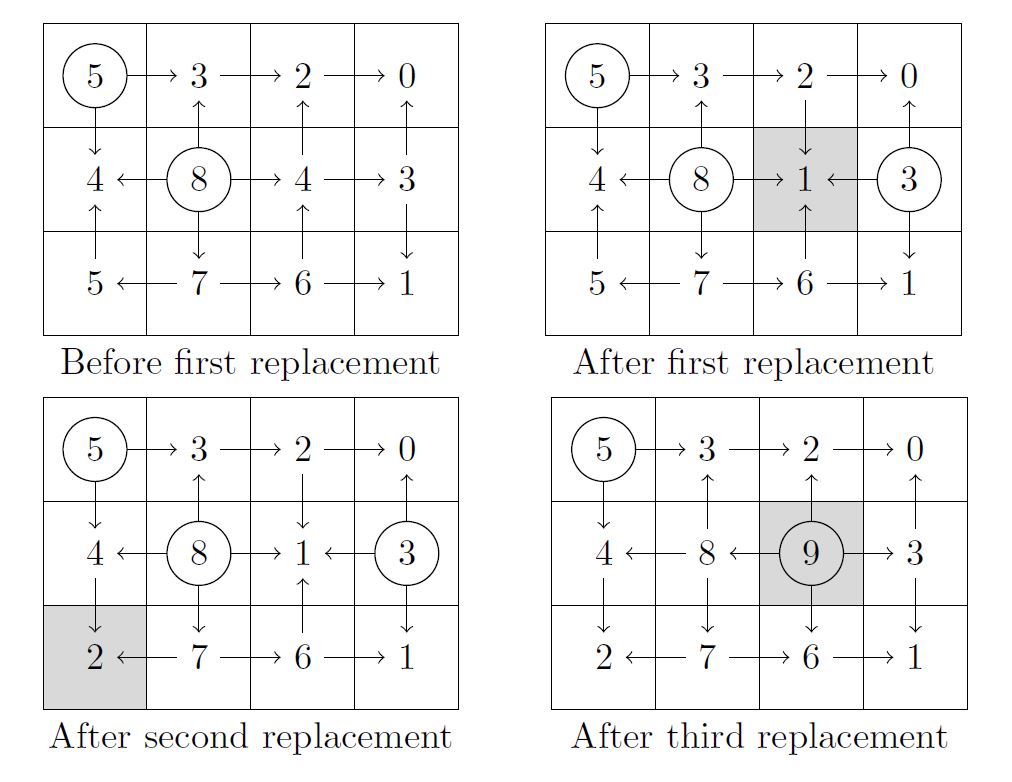
Initially, you need to pour water on the tile of height 5 and the tile of height 8. From there, the water will spread to the rest of the tiles. You can't cover the entire floor by pouring on one tile, so the answer is 2.
After the first replacement, you need to additionally pour water on the tile in the 2nd row, 4th column (which has height 3). Now the answer is 3.
After the second replacement, pouring on the same three tiles is still the best you can do.
After the last replacement, you can cover the floor by pouring on the height 5 tile and the newly added height 9 tile. The answer is 2 again.
Subtasks & Constraints
For all subtasks:- 1 ≤ R ≤ 10.
- 1 ≤ C ≤ 100,000.
- 1 ≤ Q ≤ 100,000.
- Each tile's height will always be between 0 and 1,000,000 inclusive.
- No two adjacent tiles will have the same height.
Subtasks:
- For Subtask 1 (10 points), R, C ≤ 3 and Q = 1.
- For Subtask 2 (25 points), R = 1 and Q ≤ 1000.
- For Subtask 3 (20 points), R = 1.
- For Subtask 4 (25 points), C, Q ≤ 100.
- For Subtask 5 (20 points), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 17 April 2024, 7:30pm AEST