
Problem: Graffiti
Want to try solving this problem? You can submit your code online if you log in or register.
Graffiti
Memory Limit: 32 Mb
Along your daily walk to school, there is a long pavement tiled with concrete slabs. The pavement is three slabs wide and rather long (it always feels longer on the walk home). One day you discover that some irresponsible youth has written graffiti on all these slabs. On closer inspection, you notice that it's mathematical graffiti—each slab has been marked with an integer.
This time, curiosity does not get the better of you. Instead you decide to play a game with your friends on the way to school. The game is played as follows:
- You begin by standing just before the start of the graffitied pavement.
- Each step along the pavement must land on a corner where four concrete slabs meet. By stepping on a corner, you earn points. The number of points you earn for the step is the sum of the numbers on the four slabs you have stepped on.
- You cannot step on a corner if it would include a slab that you have already stepped on before. In other words, once you have stepped on one corner of a slab, you cannot step on any other corner of that slab.
- The total number of points you earn is added up and becomes your final score.
For example, the pavement below is three slabs wide and seven slabs long. The best possible score is 50, obtained by stepping in the corners shown.
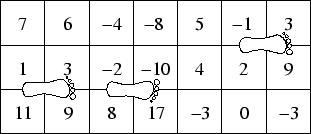
Note that you may leave any number of slabs between steps, and in fact if all slabs have negative points associated with them, you can simply opt to step on no slabs and retain a score of 0.
After several days of playing this game with your friends and consistently losing, you decide to whip out your trusty laptop to secure your place as the high scorer. Your task is to determine the highest score that can be achieved on a graffitied pavement, given the length of the pavement and the numbers on each slab.
Constraints
- 1 <= L <= 500000, where L is the length of the pavement.
Input
Your program must read from standard input. The first line of input will contain a single integer L, the length of the pavement.
Following this will be L lines in the form x y z, describing the numbers written on each of the three slabs in the given row. These three numbers will be given in order from the left side of the pavement to the right (as seen by a person who is walking), and they will all be integers between -100,000 and 100,000, inclusive.
Output
Your program must write a single line to standard output. This line must contain a single integer, giving the largest possible score you can obtain from walking along the pavement. You are guaranteed that the answer will never exceed 2,000,000,000.
Sample Input
7 7 1 11 6 3 9 -4 -2 8 -8 -10 17 5 4 -3 -1 2 0 3 9 -3
Sample Output
50
Scoring
The score for each input scenario will be 100% if the correct answer is written to the output file, and 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 26 April 2024, 4:24pm AEST