
Problem: Leaf Blower
Want to try solving this problem? You can submit your code online if you log in or register.
Leaf Blower
Output Only Task
Output File: leaf.k.out
Input files available in zip file for Linux or for Windows.
Autumn has arrived, and the leaves are falling from the trees onto your tiled courtyard. Although the leaves are pretty, your courtyard is prettier, and so you decide to clean the leaves away.
Your courtyard is formed from a grid of tiles, as illustrated below; these tiles can be described by (x,y) coordinates. The leaves have fallen into n piles, each on a different tile.
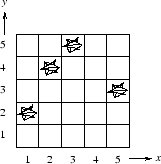
You have a leaf blower that allows you to move these piles around. The leaf blower can move a pile of leaves horizontally or vertically from one tile to another. If any two piles meet, they combine to form a single (larger) pile, which you can continue to blow around as before.
You wish to combine the leaves into a single pile using as few pile movements as you can. One pile movement involves blowing a pile of leaves (of any size) to an adjacent tile.
As an example, consider the figure below. The leaves begin in four piles, located in tiles (1,2), (2,4), (3,5) and (5,3), as seen in the first diagram.
- To begin, you could blow the two piles at (2,4) and (3,5) into the tile (3,4). This requires two pile movements. The result is that both piles join into a single pile, as shown in the second diagram.
- You could then blow the new pile at (3,4) down to (3,3), requiring one pile movement, and also blow the far right pile at (5,3) across to (3,3), requiring two more pile movements. As a result both piles merge into a single pile at (3,3), as seen in the third diagram.
- Finally, you could blow the new pile at (3,3) two tiles left and one tile down, so that it joins the pile at (1,2). This requires another three movements. At this point all of the leaves have been gathered into a single pile, as seen in the fourth diagram, and so we are done.
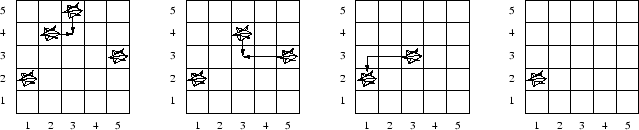
By following these steps, a total of 2+3+3=8 pile movements are used, which is the smallest number possible.
You are not required to find the best possible solution. Instead you must simply use as few pile movements as you can. Your solution will be compared against other solutions, and better solutions will score more points. See the Scoring section for details.
Input
You are given ten input files leaf.k.in (1 <= k <= 10).
The first line of each file contains the single integer n, giving the number of piles (2 <= n <= 500). Following this are n lines, each of the form x y, giving the coordinates of a single pile of leaves. All x and y coordinates are integers in the range 1 <= x,y <= 1000.
Output
For each input file leaf.k.in, you must produce an output file leaf.k.out that contains your solution.
Each solution file should contain one line for each pile movement, given in order from the first movement to the last. Each line should be of the form x y p q, which indicates that the pile at tile (x,y) is blown to the tile (p,q). These two tiles must be either horizontally or vertically adjacent, and all tile coordinates must remain in the range 1 <= x,y,p,q <= 1000.
Sample Input
4 1 2 2 4 3 5 5 3
Sample Output
3 5 3 4 2 4 3 4 3 4 3 3 5 3 4 3 4 3 3 3 3 3 2 3 2 3 1 3 1 3 1 2
Scoring
There is no "best solution" that you are required to achieve. Instead, your score for each input scenario will be determined relative to the other contestants whom you are competing against (as well as one of the judges' solutions).
For each input scenario, the contestant who finds a valid solution using the fewest pile movements will be identified. Suppose that this contestant uses p pile movements in total. Assuming your output also contains a valid solution, it will be scored as follows:
- If your solution uses between p and 1.1 x p pile movements, it will be scored according to a linear scale between 100% and 50%, where 100% corresponds to p movements and 50% corresponds to 1.1 x p movements.
- If your solution uses between 1.1 x p and 2 x p pile movements, it will be scored according to a linear scale between 50% and 10%, where 50% corresponds to 1.1 x p movements and 10% corresponds to 2 x p movements.
- If your solution uses more than 2 x p pile movements, it will be scored precisely 10%.
For example, consider an input scenario for which the best solution found by any contestant uses 100 pile movements. The scoring for a valid solution would be as follows:
| Movements | 100 | 102 | 104 | 106 | 108 | 110 | 140 | 170 | 200 | 300 | 900 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Score | 100% | 90% | 80% | 70% | 60% | 50% | 37% | 23% | 10% | 10% | 10% |
A solution that makes an invalid movement (for instance, moving to a non-adjacent square, or moving outside the allowed coordinate range of 1..1000) will score zero. Likewise, a solution that does not combine all of the leaves into a single pile will score zero.
If a solution makes an otherwise legal movement from an empty tile (i.e., there are no leaves to blow from that tile), this irrelevant movement will be silently ignored (but will add to your total number of pile movements).
Submitting for an Output Only Task
To submit your output files, you must do the following:
- Create a zip file containing all of your output files.
You may include as many or as few output files as you like (i.e.,
you do not need a solution for every input scenario). On a GNU/Linux
system you can use a command like the following:
zip mysolutions.zip leaf.*.out
On Windows systems you can create a zip file by selecting File -> New -> Compressed (zipped) Folder from within Windows Explorer, and then you can copy your output files into this new zip file.
- Submit this zip file to the FARIO website, in the same way that you would submit an ordinary solution.
The website will look inside the zip file and ensure that the output files are named correctly, although it will not check the formatting or layout of these files.
If you resubmit a different zip file, the old zip file will be deleted. For instance, suppose you submit a zip file with solutions to the first five scenarios, and later on you find a solution to the sixth. Your new submission must contain all six output files, since when you submit your new solutions the old ones will be thrown away.
Please contact the contact organisers at fario@fario.org if you have any questions about this procedure.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 9 May 2024, 7:55am AEST