Problem: House of a Thousand Blades

Want to try solving this problem? You can submit your code online if you log in or register.

House of a Thousand Blades

Input File: standard input
Output File: standard output
Time Limit: 1 second
Memory Limit: 32 MB

Seiko is a student of the katana (sword). She practises from morning to night under the watchful eye of her teacher, an old man who offers her deep wisdom hidden in cryptic sayings.

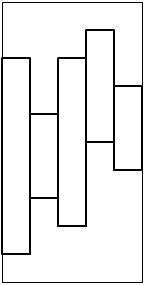
Today her teacher takes her to the koi pond and produces a flat wooden board. He carefully paints a design on the board: a series of vertical stripes of equal width. The right edge of each stripe touches the left edge of the next, with the whole design forming one contiguous shape that spans the width of the board. One such masterpiece is shown to the right.

The teacher then explains to Seiko today's lesson:

"Elegance. The swordsmaster wastes neither time nor effort. Each movement of your blade must be definite and imbued with purpose. Take your sword and carve out the shape I have painted on this board, so that it becomes a single detached piece."

Seiko's swordwork is precise, and in one cut she can carve through any straight line segment of the board, regardless of the angle of the line segment or whether its endpoints have already been cut.

Meditating on her teacher's words, Seiko realises that her task now is to find the smallest number of cuts she needs to carve out the painted shape.

Input

The first line consists of two space separated integers, W and H (1 ≤ W,H ≤ 100,000), representing the width and height of the wooden board respectively. The board can be thought of as a rectangle with co-ordinates ranging from (0,0) to (W,H).

The second line consists of W integers describing the top edges of the W brush-strokes. Each height will be between 1 and H inclusive.

The third line consists of W integers describing the bottom edges of the W brush-strokes. Each height will be between 0 and H-1 inclusive. It is guaranteed the top edge of every brush-stroke is strictly higher than its bottom edge, and that all the brush-strokes form one connected shape, i.e. for all i > 1, bottom_i < top_i-1 and bottom_i-1 < top_i.

For 40% of the available marks, N ≤ 1,000.

Output

You should output one line with one integer - the minimum number of cuts needed to obtain the desired shape from the board.

Sample Input

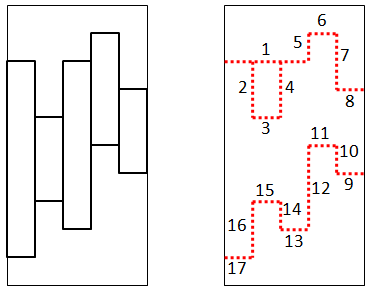
5 10
8 6 8 9 7
1 3 2 5 4

Sample Output

Explanation

The sample data corresponds to the board shown below on the left. The 17 cuts are shown on the right.

Scoring

The score for each input scenario will be 100% if the correct answer is written to the output file, and 0% otherwise.