
Problem: Shadow Architecture
Want to try solving this problem? You can submit your code online if you log in or register.
Shadow Architecture
Output File: standard output
Time Limit: 1 second
Memory Limit: 256 MB
You are an intern for an avant-garde architect renowned for their beautiful but highly unstable designs. Your current project is to relocate a mansion for a reclusive oligarch who dislikes afternoon sunlight.
The mansion to be relocated is on the eastern side of an infinitely long street. The architect has already built another mansion in a similar style on the western side of the street, which you will use for shade. Since the street is infinitely long, all positions are measured relative to a fixed point, the "end" of the street, though the street does span beyond that. Both mansions are N storeys tall, and every storey is both contiguous and has at least one metre of overlap with the storey below. Further suppose that the i-th story on the westerly mansion spans from si to ei, then a shadow will be cast on the i-th storey of your client's mansion from si to ei.
Money is no object to your client, and you may move his mansion to be anywhere along his infinitely long street. Your job now is to figure out the maximum area of your client's mansion that can be in shade.
Input
- The first line of input contains N, the number of storeys in each mansion.
- The following N lines contain two integers each. The i-th line of which is ai,bi, which indicates that the i-th storey of the west side mansion begins ai metres from the end of the street and ends bi+1 metres from the end of the street.
- The following N lines contain two integers each. The i-th line of which is ci,di, which indicates that the i-th storey of your client's mansion begins ci metres from the end of the street and ends di+1 metres from the end of the street.
Output
Output must consist of one integer, the maximum area in shade that can be achieved on your client's mansion.
Sample Input
4 2 4 2 4 2 2 1 4 1 2 2 3 3 4 1 3
Sample Output
7
Explanation
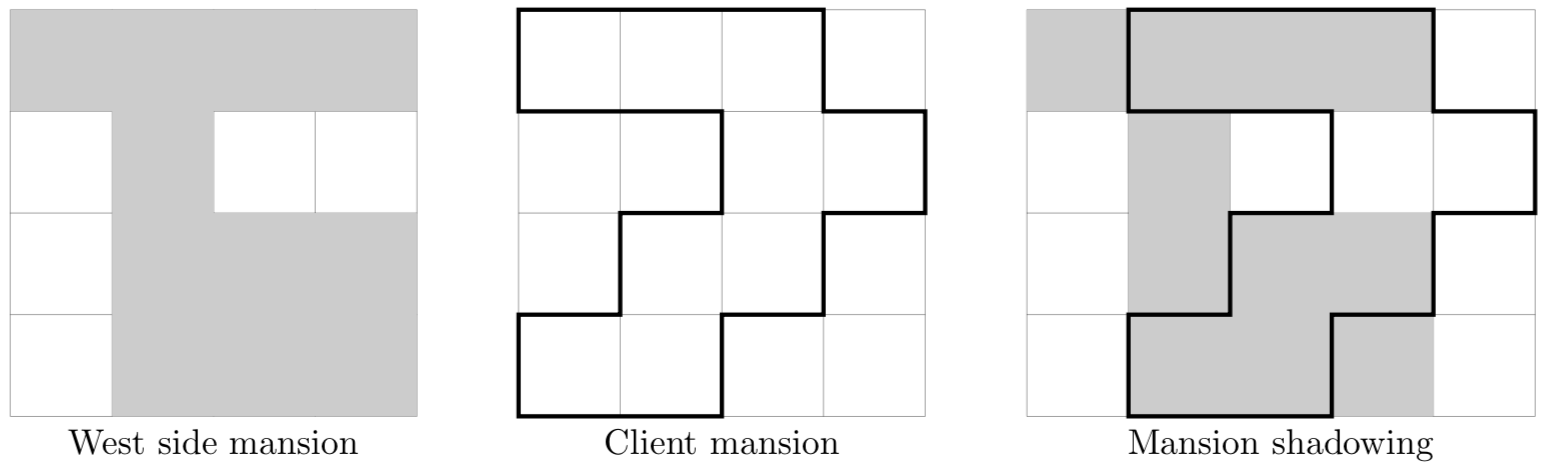
Above on the left we see the shape of the mansion on the west side of the street. This is represented in gray for the shadow it is casting. In the middle we see the shape of our client's mansion, this may be shifted arbitrarily to maximise the amount of shadow that falls on it.
By moving the client mansion one meter to the right, the entirety of its first, second and third floors are covered by afternoon shadow. This results in seven (2+2+3) units of shade falling on the client's mansion. This is the maximum amount of shade, thus the correct output is 7.
Subtasks & Constraints
For all subtasks, 1 ≤ N ≤ 100,000, 0 ≤ ai ≤ bi ≤ N, 0 ≤ ci ≤ di ≤ N.
- For Subtask 1 (30 points), 1 ≤ N ≤ 300.
- For Subtask 2 (30 points), 1 ≤ N ≤ 3000.
- For Subtask 3 (40 points), no additional constraints.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 26 April 2024, 2:19am AEST