
Problem: Train Network
Want to try solving this problem? You can submit your code online if you log in or register.
Train Network
Input File: trainin.txt
Output File: trainout.txt
Time Limit: 1 second
Memory Limit: 64 MB
The Office of Planes, Trains and Automobiles (OPTA) is responsible for the design of a new train network in the city. The train network consists of a set of train tracks where each track runs either North-South or East-West. If a North-South track and an East-West track meet at a single point, an intersection exists. For example, on the diagram below, there are six train tracks and eight intersections. At each intersection, OPTA must choose to build either an overpass or a train station.
Constructing an overpass means that trains on different tracks can run past each other without stopping. More importantly, it presents a fantastic opportunity for the sale of advertising space. As overpasses are prominent features, they can be used to hang advertisements for all to see. Furthermore, overpasses that are further out from the city centre can be built more extravagantly, hold more advertising space, and thus generate more revenue. Specifically, the city centre is at coordinates (0,0), and an overpass that is built at location (x,y) will generate |x| + |y| dollars of advertising revenue (where the notation |...| means absolute value).
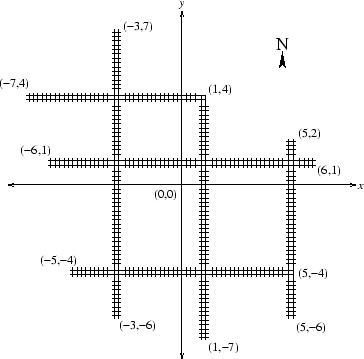
If OPTA chooses to build a train station instead of an overpass, it generates no revenue from advertising. On the other hand, it does allow commuters to hop from one track onto the other. Clearly, overpasses are much more desirable and profitable to OPTA. However commuters must be able to travel by train from any track to any other track. Therefore some train stations will still need to be constructed.
As the construction of train networks generally runs over budget and behind schedule, the chief of OPTA wishes to maximise the total revenue made from advertising. This is achieved by carefully selecting for each intersection whether to construct a train station or an overpass. The task has fallen to you to determine the maximum total revenue from overpass advertising, given a map of a train network.
Input
The first line of the input file will contain a single integer N (1 <= N <= 2,000), the number of train tracks. Each of the following N lines will describe a train track in the form x1 y1 x2 y2, where x1 y1 and x2 y2 describe the coordinates of the two endpoints of the track.
For each track, it is guaranteed that either x1 = x2 (forming a North-South track), or that y1 = y2 (forming an East-West track), but never both. It is always possible to build enough train stations so that commuters can travel from any track to any other. No two tracks running in the same direction will intersect, and all coordinates will be integers between -100,000 and 100,000 inclusive.
Output
Your output file should consist of a single line containing a single integer representing the maximum total advertising revenue that can be achieved.
Sample Input
6 -3 7 -3 -6 -7 4 1 4 -6 1 6 1 5 2 5 -6 1 4 1 -7 5 -4 -5 -4
Sample Output
23
Explanation
The sample input above corresponds to the diagram given earlier. Train stations are built at intersections (1,4), (1,1), (1,-4), (-3,1) and (5,1), and overpasses are built at intersections (-3,4), (-3,-4) and (5,-4). The total revenue is 3+4+3+4+5+4 = 23.
Scoring
The score for each input scenario will be 100% if the correct answer is output, or 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 24 April 2024, 6:15pm AEST