Problem: Friendly

Want to try solving this problem? You can submit your code online if you log in or register.

Friendly

Input File: standard input
Output File: standard output
Time Limit: 1 second
Memory Limit: 64 MB

I'm like, sooo friendly. But you already knew that. So friendly that it's actually my 43rd time at the Academy of Inclusivity and Open Communication's Summer of Empathy: the annual workshop for the nation's brightest young social engineers! Everyone loves me here; it's F-A-B. As the event draws to a close each of my fellow students knows they must be polite and trade gifts with me!

The gift trading process works as follows. First, I will acquire one of K different types of gifts (numbered from 1 to K). This will be called my starting gift. Then each of my N peers in order from 1 to N will come up to me and offer a trade: peer i will ask for a gift of type A_i and in exchange is willing to give me a gift of type B_i plus C_i chocolates (they found out my weakness during A Session). My response will be one of the following:

If I don't have a gift of type A_i, I must reject the offer.
If I have a gift of type A_i, I can choose to accept the offer. This involves surrendering my current gift and receiving a new gift of type B_i. Additionally, they will give me C_i delicious chocolates, which I will eat.
Alternately, I can reject their offer, keeping my current gift.

Note that once I have made a decision to either accept or reject an offer I will never be able to consider it again (lest I gain a reputation for being fickle and indecisive).

This afternoon I'll be heading down to the local AGI to choose my starting gift. Could you help me write a program that will tell me the maximum number of chocolates that I can possibly eat and the number of different types of starting gifts that I could choose that will allow me to achieve this maximum? Thanks so much, we can totes be BFFs after this.

Input

The first line of input will consist of two space separated integers "N K", representing the number of my fellow students and the number of types of gifts. N lines follow with the ith of these lines consisting of three space separated integers "A_i B_i C_i" representing the gift exchange offer that peer i will make to me.

Output

You should output two lines, each containing an integer: the maximum number of chocolates I can eat and the number of different types of starting gifts I could choose that will allow me to achieve this maximum.

Sample Input

Sample Output

10
2

Explanation

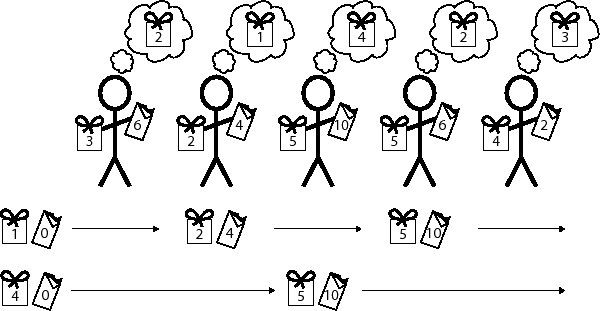
In this example I have N = 5 peers and there are K = 8 types of gifts.

Suppose I chose a starting gift of type 1. I would reject peer 1's offer (they require a gift of type 2) then trade with peer 2 for a gift of type 2 and 4 chocolates. Note that I cannot then go back to peer 1 and trade with them since I had already made a decision on their offer earlier. I could then reject the offer of peer 3 and trade with peer 4 to obtain a gift of type 5 and 6 chocolates. I must then reject peer 5's offer so I have eaten 4 + 6 = 10 chocolates in total.

Alternatively, if I chose a starting gift of type 4 then I would have to reject the offers of peers 1 and 2. I could then trade with peer 3 for a gift of type 5 and 10 chocolates. I must then reject the offers of peers 4 and 5. This means I would also have eaten a total of 10 chocolates overall.

It can be seen that in this scenario it is impossible for me to eat any more than 10 chocolates - this is the maximum number I can eat. I can do this by initially choosing one of 2 different types of starting gifts (type 1 or type 4).

Subtasks and Constraints

For all subtasks, 1 ≤ N ≤ 100,000 and 1 ≤ K ≤ 100,000. All A_i and B_i satisfy 1 ≤ A_i, B_i ≤ K and A_i ≠ B_i. All C_i satisfy 1 ≤ C_i ≤ 10,000.

For Subtask 1 (50 points), N ≤ 1,000 and K ≤ 1,000.
For Subtask 2 (50 points), no further constraints apply.

Scoring

You should always output two integers. Your score for each test case will be 100% if both integers are correct, 70% if only the first is correct, 30% if only the second is correct, and 0% if neither is correct.