
Problem: Atlantis: The Beginning
Want to try solving this problem? You can submit your code online if you log in or register.
Atlantis: The Beginning
Input File: atlanin.txt
Output File: atlanout.txt
Time Limit: 1 second
You are a geological surveyor on the peaceful island of Atlantis. It is many years yet before your island becomes famous for sinking beneath the sea; instead you are facing water problems of a less troublesome nature.
In the middle of your island is a gushing spring, which spills water down across the land. Your job is to map out the paths that this water might take.
You have with you a map of Atlantis, which divides the island into a grid of squares. For each square you have measured the height above sea level. An example of such a map is illustrated below, where the spring is located in the shaded square of height 80.
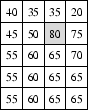
As every Atlantean knows, water can only flow downhill. In particular, water can flow from any square to any adjacent square of lower height, where adjacent squares may be to the north, south, east or west (water cannot flow across diagonals). Water cannot flow to an adjacent square of the same height; it must flow strictly downwards. If it cannot flow any further down, it forms a pool and all the local cats, llamas and unicorns come to drink and frolic. You may assume that water will never flow outside the island.
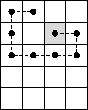
Your task is to find the longest path that the water can possibly take from the spring to a pool. For the example map given earlier, the longest path is illustrated by the dotted line below.
Input
The first line of input will contain the two integers r and c separated by a single space, where r is the number of rows in the map and c is the number of columns in the map. The rows of the map are numbered 1,2,...,r and the columns are numbered 1,2,...,c. It is guaranteed that 1 <= r,c <= 50.
The second line of input will contain the integers a and b separated by a single space, describing the location of the spring. Specifically, the spring is located in row a, column b. It is guaranteed that 1 <= a <= r and 1 <= b <= c.
Following this will be r lines, each representing a single row of the map. Each of these lines will contain c integers separated by spaces, representing the heights above sea level of the c squares in the corresponding row of the map. Each height will be an integer between 0 and 100,000 inclusive.
Output
Your output must consist of a single line containing a single integer, which is the length of the longest possible path that the water can take. You must count all squares that the water flows through, including the spring at the beginning and the pool at the end (so, for example, the path illustrated earlier has a total length of 9).
Sample Input
5 4 2 3 40 35 35 20 45 50 80 75 55 60 65 70 55 60 65 65 55 60 65 65
Sample Output
9
Scoring
The score for each input file will be 100% if the correct answer is written to the output file and 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 23 April 2024, 11:48pm AEST