
Problem: Election
Want to try solving this problem? You can submit your code online if you log in or register.
Election
Input File: elecin.txt
Output File: elecout.txt
Time Limit: 1 second
Election time is coming around, and you are lagging in the polls. Your highly-paid advisors have told you that the surest way to be re-elected is to hang an incredibly large picture of your face outside the front of the town hall — the larger the picture, the greater the votes!
You step outside and survey the front wall of the building. The wall forms a giant rectangle, containing several small rectangular windows. You cannot block anybody's view (this would surely cause a scandal), so your task is to find a rectangle on this wall with the largest possible area that does not cover any part of a window.

As an example, consider the wall illustrated above. The diagram on the left shows three windows on the wall, shaded in black. The diagram on the right shows the rectangle of largest area that you can use, shaded in grey.
Input
The first line of input will contain the integers w and h separated by a single space, where w is the width of the wall and h is the height of the wall (1 <= w,h <= 40,000). The second line of input will contain the single integer n, describing the number of windows in this wall (0 <= n <= 100).
Following this will be n lines, each describing a single window. The ith of these lines will be of the form xi yi wi hi, where xi is the distance of the window from the leftmost edge of the wall, yi is the distance of the window from the bottom edge of the wall, wi is the width of the window, and hi is the height of the window. These distances are illustrated below.
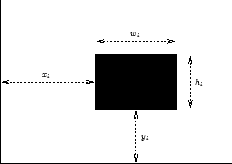
For each window, the four integers xi yi wi hi will be separated by single spaces. It is guaranteed that 1 <= xi < xi + wi <= w and 1 <= yi < yi + hi <= h. No two windows will overlap, although windows may touch at a corner or along an edge.
All distances are measured in centimetres.
Output
Your output must consist of a single line containing a single integer, giving the area of the largest possible rectangle on the wall that does not cover any part of a window. This area should be given in square centimetres.
Sample Input
800 600 3 100 250 100 150 150 180 450 20 400 500 50 50
Sample Output
180000
Explanation
The sample data above describes the example that was illustrated earlier. The rectangle of largest area that does not cover any part of a window has width 600 and height 300, and so the final area is 600 x 300 = 180,000.
Scoring
The score for each input file will be 100% if the correct answer is written to the output file and 0% otherwise.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 20 April 2024, 1:03pm AEST