
Problem: Street Construction
Want to try solving this problem? You can submit your code online if you log in or register.
Street Construction
Output File: streetout.txt
Time Limit: 1 second
Memory Limit: 1 GB
The great city of Dubvegas is designing one side of a new street. This street is divided into evenly sized chunks of land, each of which will be used for either a house or a park. The city takes great pride in both the number of parks that it has, and that no one has to walk far to reach one of their wonderful parks.
In particular, the city calls a group of consecutive houses a `block'. The size of a block is the number of houses it contains.
You must determine, given the number of chunks of land on the street and the number of parks that will be built, the minimum possible size of the largest block.
Input
The only line will contain the number of chunks of land N on the street, followed by the number of parks that will be built K.
Output
Your program should output the minimum possible size of the largest block on a street with N chunks of land, where K parks will be built.
Sample Input 1
3 1
Sample Output 1
1
Explanation 1
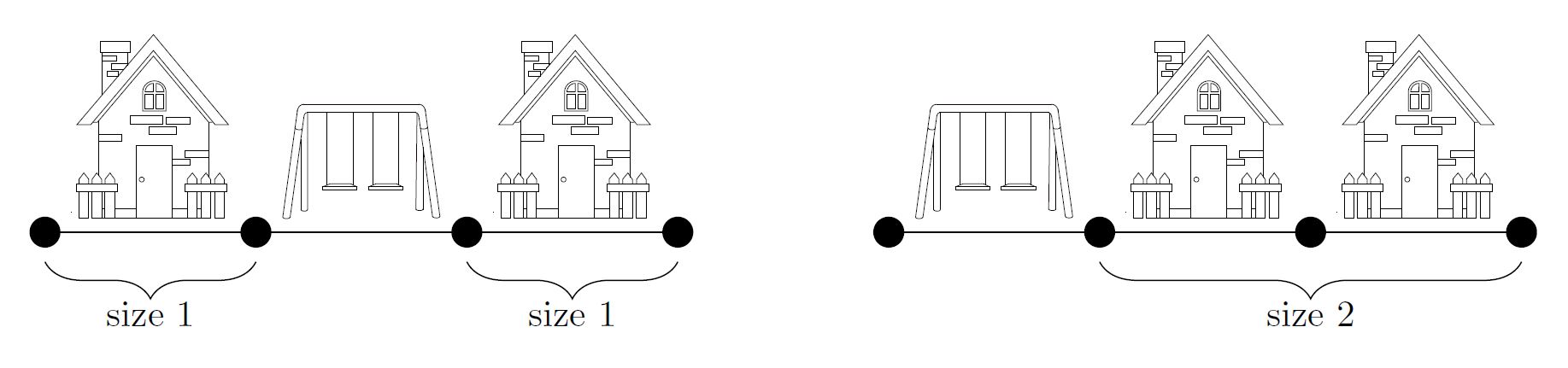
Sample Input 2
3 3
Sample Output 2
0
Explanation 2
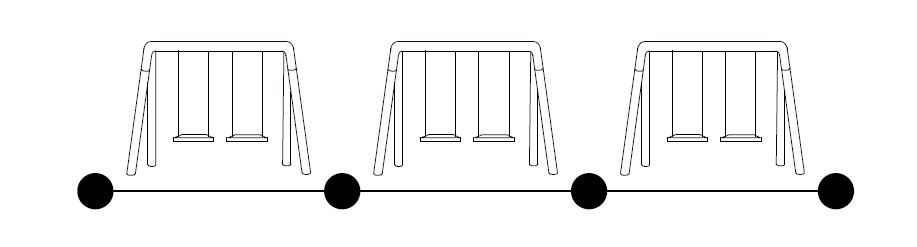
Sample Input 3
7 2
Sample Output 3
2
Explanation 3
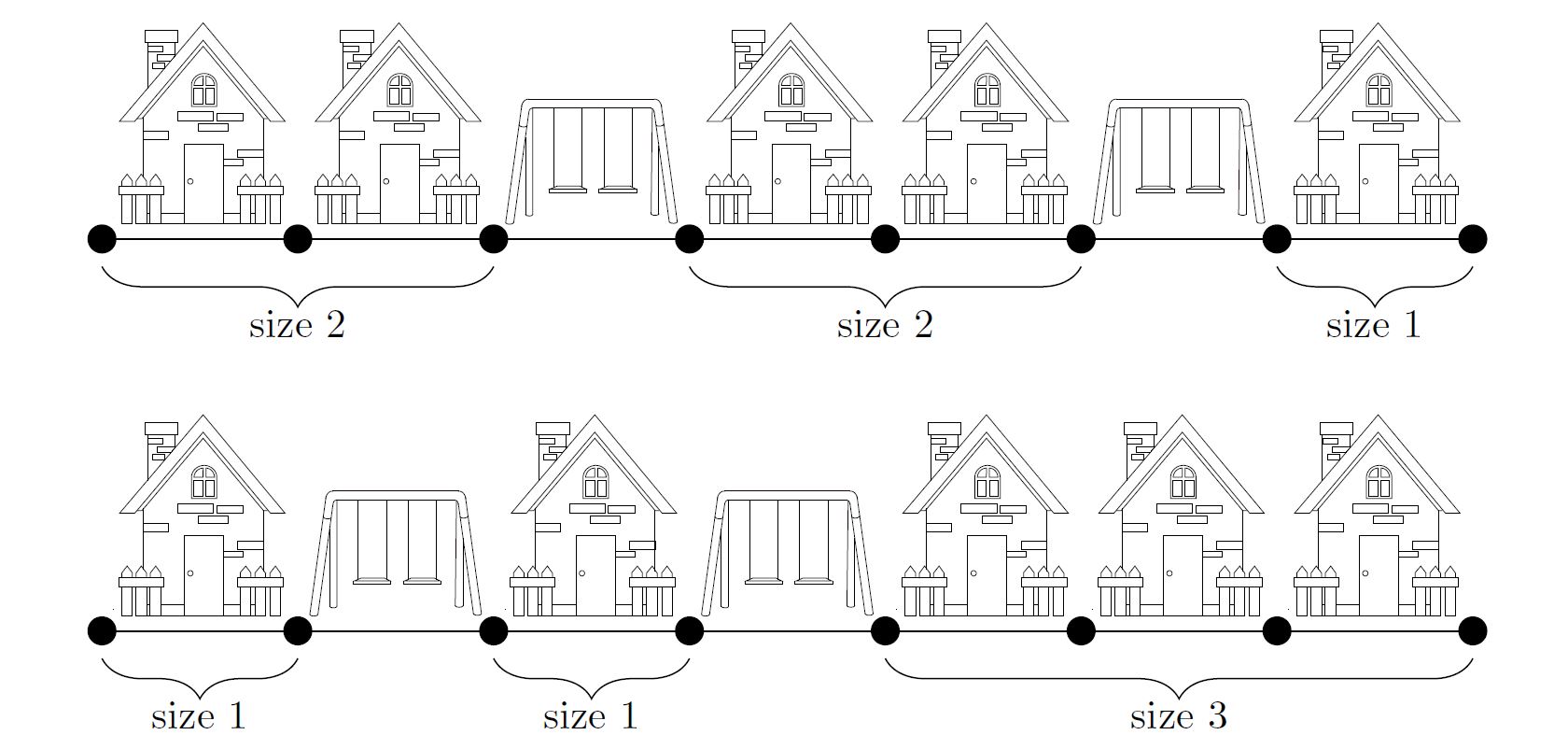
Subtasks & Constraints
For all cases, 1 ≤ K ≤ N ≤ 1,000,000,000.
- For Subtask 1 (35 marks), N ≤ 3. There will never be more than three chunks of land. You may wish to write a separate if statement for each possible case in this subtask.
- For Subtask 2 (15 marks), N = 17, K = 4. There is only one case in this subtask, where there are 17 chunks of land and 4 parks to be built. You may wish to write a separate if statement for this single case.
- For Subtask 3 (15 marks), 1 ≤ N ≤ 1,000,000,000, K = 1. There is always exactly one park to build.
- For Subtask 4 (15 marks), 2 ≤ N ≤ 100, K = 2. There are always exactly two parks to build.
- For Subtask 5 (20 marks), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 25 April 2024, 10:41pm AEST