
Problem: Evading Capture
Want to try solving this problem? You can submit your code online if you log in or register.
Evading Capture
Output File: evadingout.txt
Time Limit: 1 second
Memory Limit: 1 GB
It is the year 2077, when androids live among us, cars no longer have wheels and humans are born on blockchain. You are preparing to pull off the greatest heist of all time: stealing the Bitcoin. Stealing the Bitcoin is the easy part; evading capture is much harder.
The world consists of N cities, numbered from 1 to N. E pairs of these cities are adjacent to each other. In a single hop, you can travel from the city you are currently in to any adjacent city.
Your heist will begin in city X where the Bitcoin is located. After stealing the Bitcoin, you will need to make exactly K hops to be safe from capture (too few and the Chaser will catch you, too many and the All-Seeing I will know where you are).
You aren't yet sure which hops you will make on the day of the heist, so you have decided to work out the number of different cities you could finish in after making exactly K hops. You whip out your trusty laptop and begin coding.
Input
The first line contains the integers N, E, X and K, which are the number of cities, the number of adjacent pairs of cities, the starting city and the number of hops you must make, respectively.
Then E lines follow, describing the adjacent pairs of cities. The ith of these lines contains ai and bi, indicating that city ai is adjacent to city bi.
Output
Your program should output a single integer, the number of different cities you could finish in after making exactly K hops. You are guaranteed that at least one such sequence of hops exists.
Sample Input 1
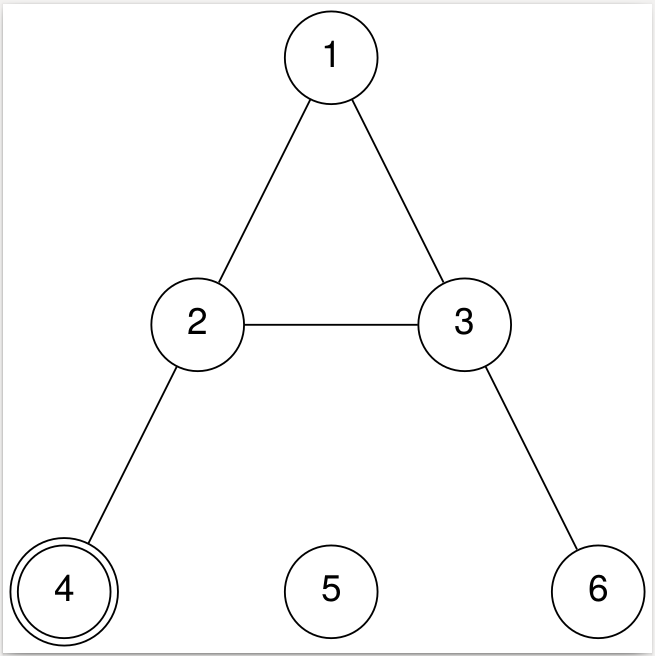
6 5 4 2 3 1 3 2 1 2 4 2 3 6
Sample Output 1
3
Sample Input 2
25 40 13 29 1 2 1 6 2 3 2 7 3 4 3 8 4 5 4 9 5 10 6 7 6 11 7 8 7 12 8 9 8 13 9 10 9 14 10 15 11 12 11 16 12 13 12 17 13 14 13 18 14 15 14 19 15 20 16 17 16 21 17 18 17 22 18 19 18 23 19 20 19 24 20 25 21 22 22 23 23 24 24 25
Sample Output 2
12

Sample Input 3
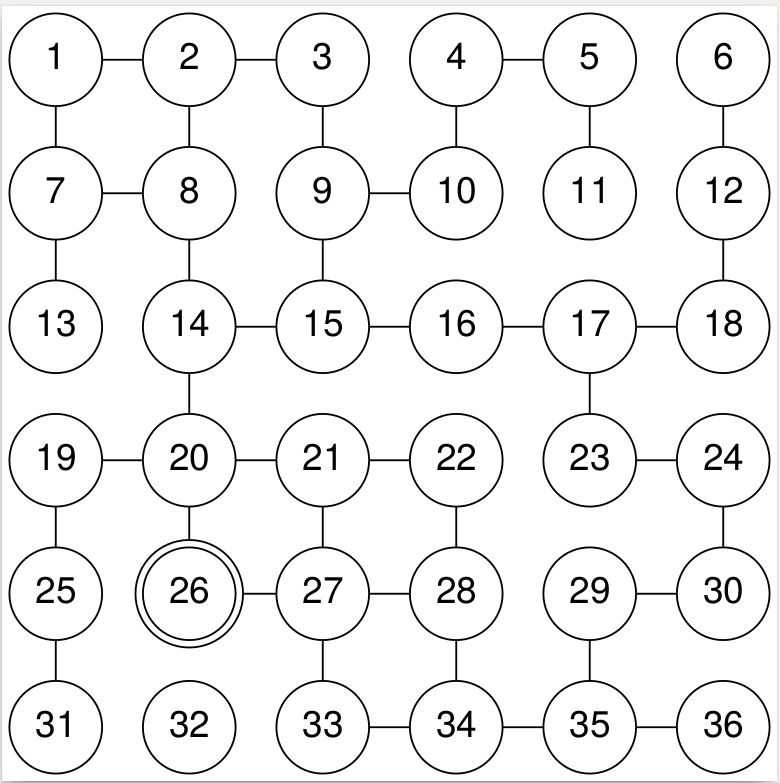
36 40 26 5 1 2 1 7 2 3 2 8 3 9 4 5 4 10 5 11 6 12 7 8 7 13 8 14 9 10 9 15 12 18 14 15 14 20 15 16 16 17 17 18 17 23 19 20 19 25 20 21 20 26 21 22 21 27 22 28 23 24 24 30 25 31 26 27 27 28 27 33 28 34 29 30 29 35 33 34 34 35 35 36
Sample Output 3
14
Explanation
In the first sample input, you start at city X = 4 and must make K = 2 hops. There are 3 different cities you could finish in, described below:
- 4 → 2 → 1
- 4 → 2 → 3
- 4 → 2 → 4
In the second sample input, you start at city X = 13 and must make K = 20 hops. The number of different cities you could finish in is 12.
In the third sample input, you start at city X = 26 and must make K = 5 hops. The number of different cities you could finish in is 14.
Subtasks & Constraints
For all cases:
- 1 ≤ N ≤ 100,000.
- 1 ≤ E ≤ 100,000.
- 1 ≤ X ≤ N.
- 1 ≤ K ≤ 1,000,000,000.
Furthermore:
- For Subtask 1 (10 marks), K = 1. That is, you must make exactly 1 hop to be safe from capture.
- For Subtask 2 (15 marks), the cities, adjacent pairs of cities, and your starting city are the same as Sample Input 2, but K may be different.
- For Subtask 3 (15 marks), the cities and the adjacent pairs of cities are the same as Sample Input 2, but K and X may be different.
- For Subtask 4 (35 marks), the cities and the adjacent pairs of cities are the same as Sample Input 3, but K and X may be different.
- For Subtask 5 (15 marks), N ≤ 50.
- For Subtask 6 (10 marks), no further constraints apply.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 27 April 2024, 9:59am AEST