
Problem: Frequent Flyer
Want to try solving this problem? You can submit your code online if you log in or register.
Frequent Flyer
Output File: standard output
Time Limit: 1 second
Memory Limit: 256 MB
Congratulations! You've just become an official card-carrying member of Flagship Air Rewards.
Here at Flagship Air we serve N different cities (numbered from 1 to N) helping you to travel to wherever your heart leads you. We operate a single flight in one direction between every pair of cities. Specifically, between every pair of distinct cities i and j, we either operate a flight from i to j, or, from j to i; but not both. To thank you for your loyalty, every time you fly with us we will credit points to your account depending on which flight you take. See the Input section below for details.
To help you kickstart your account, we highly recommend you to relax on a "Flagship Trip". A "Flagship Trip":
- Starts in a city of your choosing;
- Ends in a different city;
- Uses exactly N-1 Flagship Air flights to move between cities; and
- Visits each of the N cities precisely once.
As we understand that you may be far too lazy to plan out your own "Flagship Trip" by hand, we encourage you to write a program that does this for you. Additionally, your program should attempt to maximise the total number of points that you will accrue over the entire course of the trip.
Please note that your program does not have to find the optimal "Flagship Trip" in every case; see the Scoring section below for details.
We look forward to flying with you soon!
Input
- The first line of input will contain one integer N, representing the total number of cities that Flagship Air flies between.
- The following N lines of the input will each contain N integers separated by spaces. The jth integer on the ith of these lines contains -1 if there is no Flagship Air flight from i to j and the number of points gained by taking this flight, otherwise.
Between every distinct pair of cities, the direction of the flight between them is determined uniformly at random (there is a 50% chance that the flight will go in either direction). Additionally, for every flight the number of points available on it is a uniformly random integer between 0 and 1000000, inclusive.
Output
Your program must output N lines each containing exactly one integer. These lines describe a valid "Flagship Trip". The kth of these lines should contain a single integer: the number of the kth city visited on the trip. Each integer from 1 to N should appear precisely once in the output.
Sample Input
4 -1 15 -1 -1 -1 -1 59 -1 79 -1 -1 60 40 83 -1 -1
Sample Output
4 2 3 1
Explanation
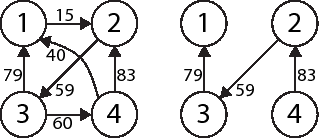
By examination of all possible "Flagship Trips", we find that we collect the most points by going from 4 to 2, 2 to 3, and finally 3 to 1. This trip scores 83+59+79 = 221 for its flights. Please note that this sample input was not generated according to the random procedure described in the Input section above and thus will not be used for grading.
Subtasks & Constraints
For all subtasks, 2 ≤ N ≤ 100.
- For Subtask 1 (20 points), 2 ≤ N ≤ 10.
- For Subtask 2 (80 points), no additional constraints.
Scoring
For each test case, if your program does not output a valid trip, it will score 0%. Otherwise, your score will be determined from the number of points gained by following your program's trip and the number of points gained by following the judges' trip. Specifically, if your trip gains x points and the judges' trip gains y points then your score (as a percentage) is calculated as:
Where the mathematical constant e = 2.71828. Note that for each test case:
- A valid trip always scores at least 20%; and
- The judges' trip scores 100%.
Privacy
statement
© Australian Mathematics Trust 2001-2024
Page generated: 26 April 2024, 6:51pm AEST