Problem: Optimal Delivery

Want to try solving this problem? You can submit your code online if you log in or register.

Optimal Delivery

Time Limit: 8 seconds
Memory Limit: 256 MB

Module (courier.h)
Module (courier.c)
Template (C)
Template (C++)

You have just moved to a new city, and started a job as a courier with OPTIMAL DELIVERY. The city is laid out on a grid of squares with R rows and C columns, with squares labelled from (0, 0) in the north-west corner to (R-1, C-1) in the south-east corner. It is only possible to travel between squares that are adjacent either horizontally or vertically.

Being new here, you haven't quite figured out the travel times between squares. A more experienced colleague tells you that all the travel times were chosen uniformly at random between 0 and 1 minute when the city was built, and have since been kept constant for tax purposes.

In order to avoid embarrassing your employer, you must first complete some mandatory training. You are to propose up to Q routes (one at a time), each between any two squares of your choice, and you will be told how much longer your route takes than the fastest route between those two squares.

Once you have completed your training, you will be asked to deliver a series of M parcels. For each parcel, you will be told the pickup square and the destination square. For each parcel, you may assume that the pickup square was chosen uniformly at random among all R*C squares in the city and that the destination square was then chosen uniformly at random among the remaining R*C-1 squares in the city. You must propose a route to deliver the parcel as fast as you can. You will be given points based on how much longer your route takes than the fastest route between those two squares.

Be warned though, OPTIMAL DELIVERY has high expectations of its new recruits, and will immediately fire you if you propose a route that passes through the same square more than once, or a route that passes outside the city grid, both during training and on the job.

Input / Output

This task has no input or output files. Instead your solution must interact with the functions the header file "courier.h". The provided functions are described in detail in the next section.

Do not output anything to stdout, or you will receive 0 points for the test case.

Module

Your program must interact with functions in "courier.h" as follows:

Do not implement a main function -- this is provided by the module. Instead, implement the function
void init(int R, int C, int M, int Q)
This function will be called exactly once after your program is launched. From this function, you are permitted to make up to Q calls to the function
double query(int rStart, int cStart, int length, const char* path)
where:
- rStart and cStart are the row and column of the square in which your proposed route starts,
- length is the length of the route (the number of times you move between squares), and
- path is a string consisting only of characters N, E, S, and W, representing north, east, south, or west movements, respectively.
The query function will return how much longer, in minutes, your proposed route is than the fastest one. Each call to the query function takes time linearly proportional to length¹.
You must also implement the function
void solve(int rStart, int cStart, int rEnd, int cEnd, int* length, char* path)
After your init function returns, this function will be called M times, representing the M deliveries you must make.
- rStart and cStart are the row and column of the square in which you must pick up the parcel,
- and rEnd and cEnd are the row and column of the square to which the parcel must be delivered.
Note: the squares (rStart, cStart) and (rEnd, cEnd) will not be the same.
Note: For each call made to solve, we will guarantee that (rStart, cStart) was chosen uniformly at random among all R*C squares in the grid and that (rEnd, cEnd) was then chosen uniformly at random among the R*C-1 remaining squares in the grid.
You must return a valid path between these given endpoints by setting *length = L, where L is the length of your proposed route, and filling the array path with exactly L characters representing the movements between squares required to reach the destination, in the same format as described above. L must not exceed R C - 1.
Your solution will receive points based on how much longer your proposed routes take than the fastest ones. See the Scoring section below for further details.

Experimentation

In order to experiment with your code on your own machine, first download the provided courier.h and courier.c files to the same folder as your code file, and add #include "courier.h" to the top of your code. A sample solution is also available to assist you. Compile your C solution with

gcc -O2 -Wall -static yourcode.c courier.c -o courier -lm

or, if you use C++,

g++ -std=c++11 -O2 -Wall -static yourcode.cpp courier.c -o courier

where yourcode.c/cpp is the name of your code file. Note that you should still use courier.c even if your solution is in C++. The compiled executable courier will read 4 whitespace-separated integers R C M Q from standard input, followed by 2R-1 lines describing the travel times, where even-numbered lines contain C-1 whitespace-separated decimal numbers between 0 and 1 (inclusive), and odd-numbered lines contain C whitespace separated decimal numbers between 0 and 1 (inclusive). This should be followed by M lines of the form R_{S_i} C_{S_i} R_{E_i} C_{E_i}, where (R_{S_i}, C_{S_i}) is the starting square and (R_{E_i}, C_{E_i}) is the ending square for the ith call that the module will make to the solve function. Such an input file will look something like this:

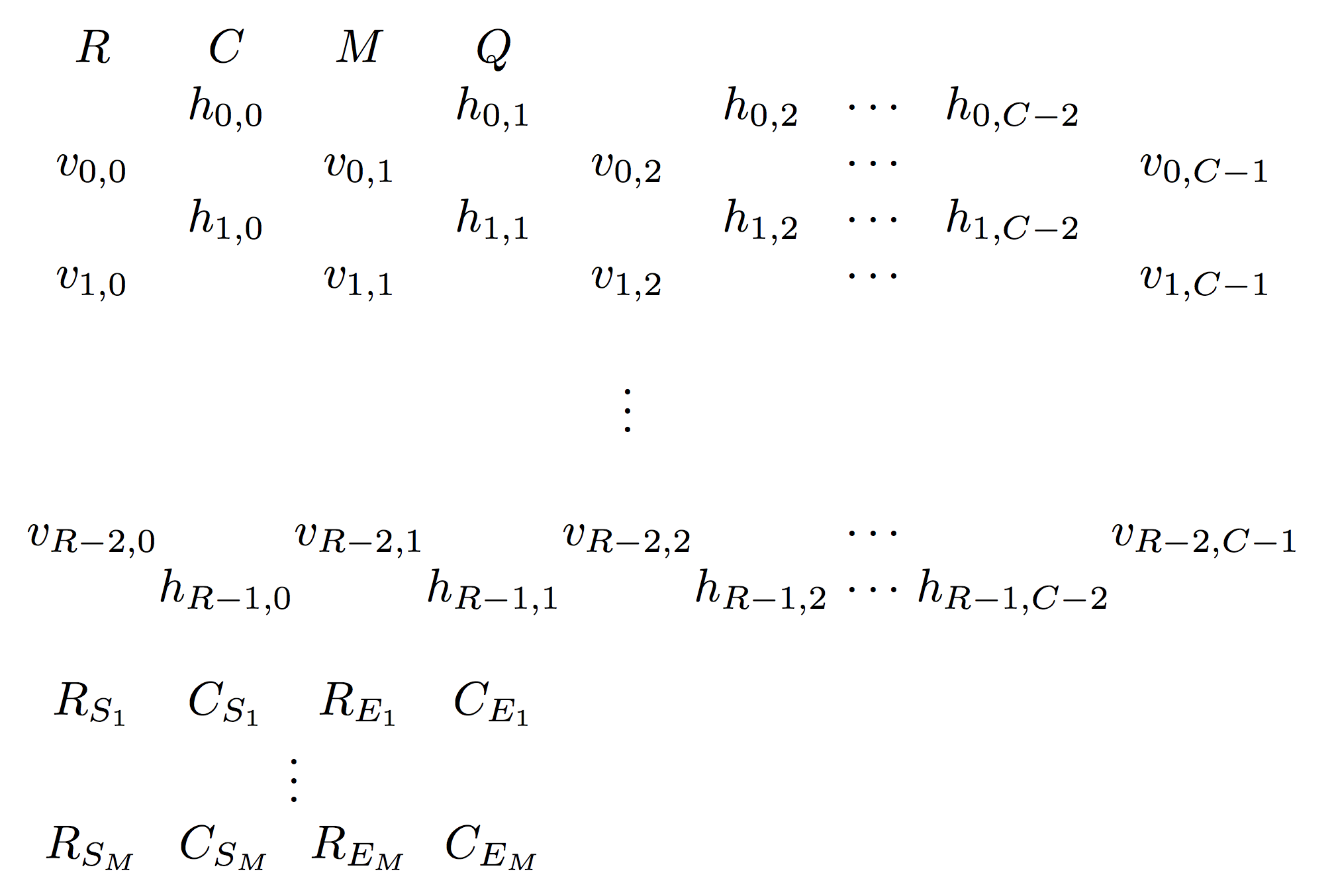
where h_{i, j} is the travel time between square (i, j) and square (i, j+1), and v_{i, j} is the travel time between square (i, j) and square (i+1, j).

Note: the input as illustrated here contains extra whitespace for clarity. This is not required by the module, but will be safely ignored if provided.

The executable will print M lines to standard output, where the ith line contains a decimal number s_i, the score your program receives for query i. This will be followed by a line containing Total score: S, where S is the total score for the test case. See the Scoring section for more details.

Sample Input

3 4 1 2
    0.5     1.0     0.9
0.1     0.6     0.7     0.4
    0.0     1.0     0.3
0.3     0.2     0.4     0.6
    0.0     1.0     0.5

2 1 0 2

Sample Session

The module calls init(3, 4, 1, 2).
You call query(0, 0, 3, "EEE"). The function returns 0.6 since the proposed route takes 2.4 minutes, while the fastest possible route "SEEEN" takes 1.8 minutes.
You call query(1, 0, 2, "ES"). This path takes 0.2 minutes and is the fastest route, so the function returns 0.
Your init function returns.
The module calls solve(2, 1, 0, 2, &length, path), as specified in the input, asking you to find as quick a route as you can between squares (2, 1) and (0, 2).
You set *length = 3 and path[0] = `N', path[1] = `E', path[2] = `N'. The module outputs 33 to standard output, the score for this query.
The module outputs Total score: 33 to standard output, the total score for this test case.

Subtasks & Constraints

For all calls to solve, 0 ≤ rStart, rEnd < R and 0 ≤ cStart, cEnd < C, and length and path will always be non-NULL pointers. Also note that for all cases within a subtask, the values of R, C, M and Q are fixed, as specified:

For Subtask 1 (30 points), R = 2, C = 10, M = 1000, Q = 5000.
For Subtask 2 (15 points), R = C = 10, M = 1000, Q = 25000.
For Subtask 3 (15 points), R = C = 50, M = 1000, Q = 25000.
For Subtask 4 (20 points), R = C = 50, M = 1000, Q = 4999, and all travel times are either 0 or 1.
For Subtask 5 (20 points), R = C = 50, M = 1000, Q = 5000.

Scoring

Your score for this problem will be the maximum score among all your submissions to the problem. For each submission, your score for each subtask will be the minimum score among all test cases in that subtask. Your score for each test case will be

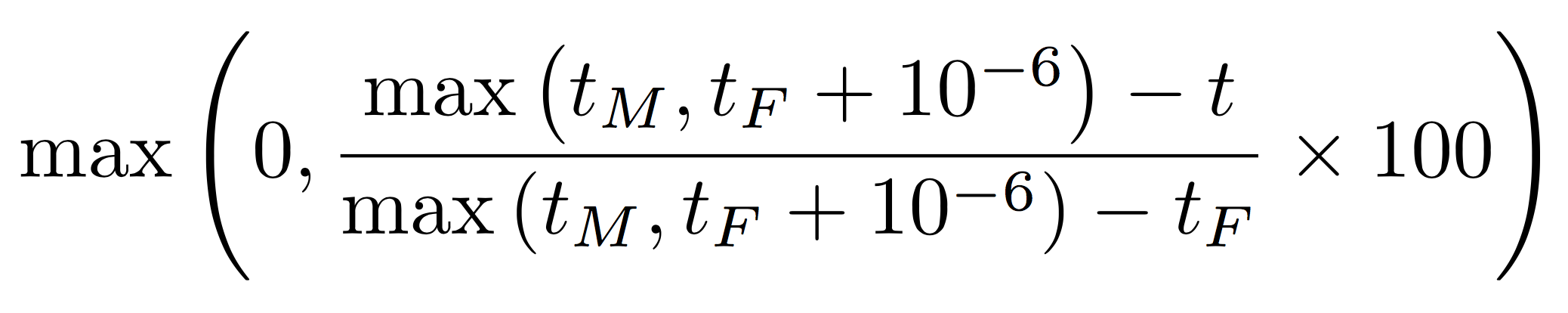
where t, t_F, and t_M are the sums of all t_i, t_F_i, and t_M_i, respectively. For the ith call to solve:

t_i is the time taken by your proposed route,
t_F_i is the time taken by the fastest possible route, and
t_M_i is the mean of the time taken by the route which travels first in the north-south direction to the destination's grid row, then in the east-west direction to the destination; and the route which travels first in the east-west direction to the destination's grid column, then in the north-south direction to the destination.

If you propose a route that results in you being fired, you will receive 0 points for the test case.

If you output anything to stdout, you will receive 0 points for the test case.