Problem 3 - Off the Track

We will discuss the solution to Off the Track from AIO 2025.

Solution

Subtask 1: The best solution involves yelling the same instruction over and over

There are two options: either we yell forwards over and over or we yell backwards over and over:

• If we yell forwards over and over then student 1 will be the last person to leave the track. This takes L-P₁ seconds.
• If we yell backwards over and over then student N will be the last person to leave the track. This takes P_N seconds.

Subtask 2: N = 2

The two options from subtask 1 are also options for this subtask: specifically, if we yell forwards over and over it will take L-P₁ seconds and if we yell backwards over and over it will take P₂ seconds. But there are other options too.

Let's look at sample input 2 where N = 2, L = 7, P₁ = 2 and P₂ = 6. If we yell forwards over and over it will take L-P₁ = 5 seconds and if we yell backwards over and over then it will take P₂ = 6 seconds. But the answer for this case is 4 seconds, if we yell backwards once (to remove student 1 from the track) and then yell forwards 3 times (to remove student 2 from the track). This is shown below:

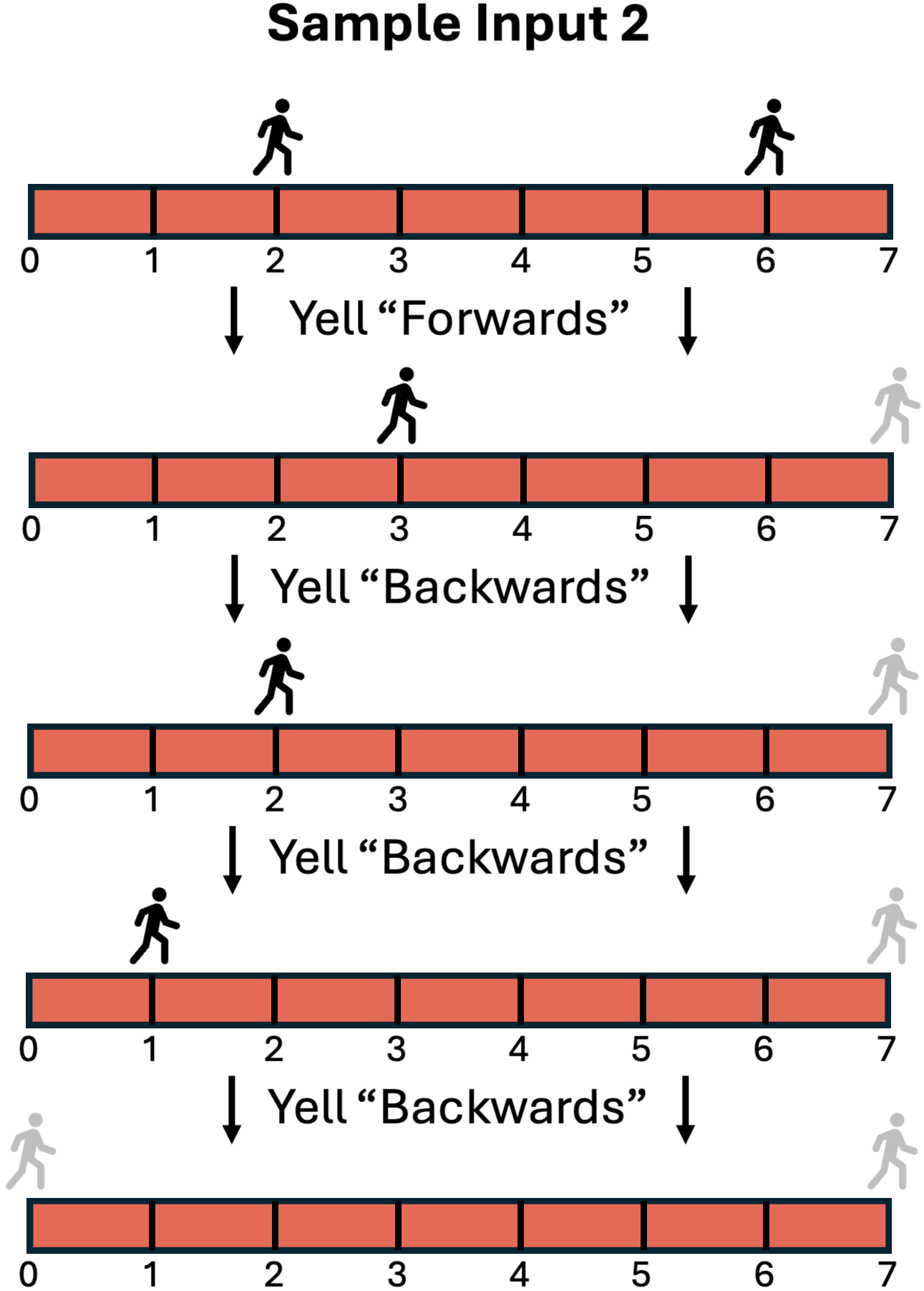
We can turn this into a general strategy:

• We yell forwards L - P₂ times to remove student 2 from the track.
• Student 1 is now at location P₁ + (L - P₂) and so we can yell backwards P₁ + (L - P₂) times to remove student 1 from the track.
• This takes L - P₂ + P₁ + (L - P₂) seconds. We can rearrange this to P₁ - 2P₂ + 2L.

• We yell backwards P₁ times to remove student 1 from the track.
• Student 2 is now at location P₂ - P₁ and so we can yell forwards L - (P₂ - P₁) times to remove student 2 from the track.
• This takes P₁ + L - (P₂ - P₁) seconds. We can rearrange this to 2P₁ - P₂ + L.

1. Only yell forwards: L-P₁ seconds.
2. Only yell backwards: P₂ seconds.
3. Yell forwards and then backwards: P₁ - 2P₂ + 2L seconds.
4. Yell backwards and then forwards: 2P₁ - P₂ + L seconds.

Full Solution

We can use the four options from subtask 2 for the full solution. However, the third and fourth aren't as clear anymore. For example, consider the third option where we yell forwards and then backwards. In subtask 2 we yelled forwards enough times to remove student 2 from the track and then yelled backwards enough times to remove student 1 from the track. But what do we do if there are 3 students? We could yell forwards enough times to remove student 3 from the track and then yell backwards enough times to remove both student 1 and 2 from the track, or we could yell forwards enough times to remove students 3 and 2 from the track and then yell backwards enough times to remove student 1 from the track. Which of these is better? This depends on the test case! (as an exercise, design some of your own test cases and try these options).

In general, the third option from subtask 2 gives rise to N-1 options in this subtask:

• We yell forwards enough times to remove the last student (student N) from the track and then yell backwards enough times to remove the first N-1 students from the track. This involves yelling forwards L - P_N times and backwards P_N-1 + (L - P_N) times.
• We yell forwards enough times to remove the last two students from the track and then yell backwards enough times to remove the first N-2 students from the track. This involves yelling forwards L - P_N-1 times and backwards P_N-2 + (L - P_N-1) times.
• We yell forwards enough times to remove the last three students from the track and then yell backwards enough times to remove the first N-3 students from the track. This involves yelling forwards L - P_N-2 times and backwards P_N-3 + (L - P_N-2) times.
• ...
• We yell forwards enough times to remove the last N-1 students from the track and then yell backwards enough times to remove the first student from the track. This involves yelling forwards L - P₂ times and backwards P₁ + (L - P₂) times.

We can do similar calculations for the fourth option from subtask 2 which also gives rise to N-1 options in this subtask. Try to work out the ith option yourself and check back here.

This solution has a time complexity of O(N) which is fast enough to score 100.

Code

Below you can see the full solution written in Python and C++. I suggest trying to code the solution yourself and only look at our code after you finish or if you get stuck.

• Python 3
• C++

# N is the number of students.
N = 0
# L is the length of the track.
L = 0

# P contains the locations of the students. Note that the list starts from 0,
# and so the values are P[0] to P[N-1].
P = []

# Read the values of N, L, and the student locations.
N, L = map(int, input().strip().split())
P = list(map(int, input().strip().split()))

# Compute the solution
answer = min(L-P[0], P[N-1]) # option 1 and 2

for i in range(N-1):
  answer = min(answer, P[N-i-2] - 2*P[N-i-1] + 2*L) # option 3 with some slight adjustments because the list is indexed starting from 0 not 1
  answer = min(answer, 2*P[i] - P[i+1] + L) # option 4 with some slight adjustments because the list is indexed starting from 0 not 1

print(answer)

#include <cstdio>
#include <algorithm> // for std::min

/* N is the number of students. */
int N;
/* L is the length of the track. */
int L;

/*
 * P contains the locations of the students. Note that the array starts from 0,
 * and so the values are P[0] to P[N-1].
 */
int P[200005];

int main(void) {
  /* Read the values of N, L, and the student locations. */
  scanf("%d%d", &N, &L);
  for (int i = 0; i < N; i++) {
    scanf("%d", &P[i]);
  }

  /* Compute the solution */
  int answer = std::min(L-P[0], P[N-1]); // option 1 and 2

  for (int i = 0; i < N-1; i++) {
    answer = std::min(answer, P[N-i-2] - 2*P[N-i-1] + 2*L); // option 3 with some slight adjustments because the list is indexed starting from 0 not 1
    answer = std::min(answer, 2*P[i] - P[i+1] + L); // option 4 with some slight adjustments because the list is indexed starting from 0 not 1
  }
  
  printf("%d\n", answer);
}

Click here to go back.